Weir

**Figure 121:** Weir geometry
$\begin{figure}\epsfig{file=Weir.eps,width=10cm}\end{figure}$

A wear is a structure as in Figure 121 at the upstream end of a channel. The weir can occur in different forms such as broad-crested weirs (left picture in the Figure) and sharp-crested weirs (right picture in the Figure). The wear element in CalculiX can be used to simulate the part of the wear to the left of the highest point, which is the point at which critical flow is observed. The part to the right of this point (denoted by “L” in the figure) has to be modeled by a straight channel element with high slope or by a step element with negative step size (i.e. drop).

The volumetric flow can be characterized by a law of the form

$\displaystyle Q=C b (h-p)^{3/2},$

(178)

where C is a constant. For instance, in the formula by Poleni $C=2 C_d \sqrt{2 g}/3$ , where is coefficient smaller than 1 to be measured experimentally [12]. The flow across a wear corresponds to the flow underneath a sluice gate with infinite depth underneath the gate and critical conditions, therefore (Equation (175), for $\theta=0$ and ):

$\displaystyle Q=C^* b h_c \sqrt{2 g (h-h_c)},$

(179)

where now satisfies (by equating to the above equations and taking and ):

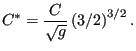$\displaystyle C^* = \frac{C}{\sqrt{g} } \left( 3/2 \right ) ^ {3/2}.$

(180)

The following constants have to be specified on the line beneath the *FLUID SECTION,TYPE=CHANNEL WEIR card (the width, the trapezoid angle, the slope and the grain diameter should be the same as for the downstream element immediately next to the weir; they are needed for the calculation of the critical height and normal height):

the width
the trapezoid angle $\theta$
not used
the slope $S_0 = \sin \phi, -1<S_0<1$ (for this element the slope must be
the grain diameter for the White-Colebrook law or the Manning constant for the Manning law (in the latter case the user has to specify the parameter MANNING on the *FLUID SECTION card)
the height of the weir
the weir constant

A wear can only be used at the upstream end of a channel. A wear in the middle of a channel has to be modeled by a step followed by a drop.

Example files: channel7.