Beam knot

The expansion of a single beam node leads to a planar set of nodes. Therefore, the stretch of a knot based on this expansion is reduced to the stretch along the two principal directions in that plane. The stretch in the direction of the beam axis is not relevant. Let us assume that $\boldsymbol{T_1}$ is a unit vector tangent to the local beam axis and $\boldsymbol{E_1}, \boldsymbol{E_2}$ are two unit vectors in the expansion plane such that $\boldsymbol{E_1} \cdot \boldsymbol{E_2} =0$ and $\boldsymbol{E_1} \times \boldsymbol{E_2} = \boldsymbol{T_1}$. Then, the stretch in the plane can be characterized by vectors $\boldsymbol{T_2}$ and $\boldsymbol{T_3}$ along its principal directions:

$$\boldsymbol{T_2} = \xi ( \boldsymbol{E_1} \cos \varphi + \boldsymbol{E_2} \sin \varphi)$$ (218)

$$\boldsymbol{T_3} = \eta ( -\boldsymbol{E_1} \sin \varphi + \boldsymbol{E_2} \cos \varphi)$$ (219)

leading to three stretch degrees of freedom $\varphi$, $\xi$ and $\eta$. $\varphi$ is the angle $\boldsymbol{T_2}$ makes with $\boldsymbol{E_1}$, $\xi$ is the stretch along $\boldsymbol{T_2}$ and $\eta$ is the stretch along $\boldsymbol{T_3}$. The right stretch tensor $\boldsymbol{U}$ can now be written as:

$$\boldsymbol{U} =\boldsymbol{T_1} \otimes \boldsymbol{T_1}+\boldsymbol{T_2} \otimes \boldsymbol{T_2}+\boldsymbol{T_3} \otimes \boldsymbol{T_3}$$

$$=\boldsymbol{T_1} \otimes \boldsymbol{T_1}+(\xi^2 \cos^2 \varphi ... ...in^2 \varphi + \eta^2 \cos^2 \varphi) \boldsymbol{E_2} \otimes \boldsymbol{E_2}$$

$$+ (\xi^2-\eta^2)\cos \varphi \sin \varphi (\boldsymbol{E_1} \otimes \boldsymbol{E_2}+\boldsymbol{E_2} \otimes \boldsymbol{E_1}).$$ (220)

The rotation vector reads in component notation

$$R_{ij}=\delta_{ij} \cos \theta + \sin \theta e_{ikj} n_k + (1 - \cos \theta ) n_i n_j.$$ (221)

Here, $\boldsymbol{\theta}$ is a vector along the rotation axis satisfying $\boldsymbol{\theta}=\theta \boldsymbol{n}$, $\Vert\boldsymbol{n}\Vert=1$. Assuming that at some point in the calculation the knot is characterized by $(\boldsymbol{w_0},\boldsymbol{\theta_0},\varphi_0,\xi_0,\eta_0)$, a change $(\boldsymbol{\Delta w},\boldsymbol{\Delta \theta},\Delta \varphi,\Delta \xi,\Delta \eta)$ leads to (cf. Equation (216)):

$$\boldsymbol{u_0+\Delta u }=\boldsymbol{w_0+\Delta w}+[ \boldsymbo... ... \eta_0 + \Delta \eta) - \boldsymbol{I}] \cdot (\boldsymbol{p}-\boldsymbol{q}).$$ (222)

Taylor expansion of $\boldsymbol{R}$:

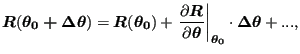$$\boldsymbol{R} (\boldsymbol{\theta_0+\Delta \theta})=\boldsymbol{... ...}} \right \vert _{\boldsymbol{\theta_0}} \cdot \boldsymbol{\Delta \theta}+ ...,$$ (223)

and similar for $\boldsymbol{U}$ and keeping linear terms only leads to the following equation:

$$\boldsymbol{\Delta u }= \boldsymbol{\Delta w}+\left[ \left. \frac {\partial \boldsymbol{R... ... \boldsymbol{U}(\varphi_0, \xi_0, \eta_0) \cdot (\boldsymbol{p}-\boldsymbol{q})$$

$$+ \boldsymbol{R} (\boldsymbol{\theta_0}) \cdot \left[ \left. \fra... ...right \vert _{\eta_0} \Delta \eta \right] \cdot (\boldsymbol{p}-\boldsymbol{q})$$

$$+ \boldsymbol{w_0}+[\boldsymbol{R} (\boldsymbol{\theta_0}) \cdot ... ...ta_0) - \boldsymbol{I}] \cdot (\boldsymbol{p}-\boldsymbol{q})-\boldsymbol{u_0}.$$ (224)

The latter equation is a inhomogeneous linear equation linking the change in displacements of an arbitrary node belonging to a knot to the change in the knot parameters (translation, rotation and stretch). This equation is taken into account at the construction phase of the governing equations. In that way the expanded degrees of freedom, being dependent, never show up in the equations to solve.