Next: Materials Up: Boundary conditions Previous: Face-to-Face Mortar Contact Contents
The massless node-to-face contact formulation has been introduced in CalculiX in order to model perfectly hard contact within explicit dynamic calculations. The implementation closely follows [69].
For the sake of simplicity, frictionless contact is taken as example. Let ![]() denote the gap,
denote the gap, ![]() is the contact force.
is the contact force.
For a zero contact force the gap can be any positive real number including zero
(
![]() ), for a strictly positive force the gap is zero and a negative contact
force is not plausible (i.e. no adhesion is assumed). These
dependencies can be represented in the form of
), for a strictly positive force the gap is zero and a negative contact
force is not plausible (i.e. no adhesion is assumed). These
dependencies can be represented in the form of
![]() as in Figure
135. For dynamic calculations with friction the gap
velocity
as in Figure
135. For dynamic calculations with friction the gap
velocity
![]() is used in the contact laws. In principle, the gap
velocity can be positive or negative. Indeed, if an object is approaching an
obstacle the gap decreases and the velocity is negative. After collision the
gap is increasing and the velocity is positive. However, at collision
(i.e.
is used in the contact laws. In principle, the gap
velocity can be positive or negative. Indeed, if an object is approaching an
obstacle the gap decreases and the velocity is negative. After collision the
gap is increasing and the velocity is positive. However, at collision
(i.e. ![]() )
)
![]() is satisfied (the gap remains zero for static
equilibrium or is increasing after a collision) and now Figure
135 also applies for
is satisfied (the gap remains zero for static
equilibrium or is increasing after a collision) and now Figure
135 also applies for
![]() . In order for the velocity
to be strictly positive, the force has to be zero.
. In order for the velocity
to be strictly positive, the force has to be zero.
Now, a couple of mathematical concepts are introduced. For further details the reader is referred to [52] and [102].
| (322) | |||
| (323) |
The admissible set on which ![]() is defined is
is defined is
![]() .
.
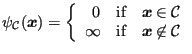 |
(324) |
So the indicator function is zero for all elements included in the set
and infinity else. The indicator function for
![]() is shown
in Figure 136 (bold line)
is shown
in Figure 136 (bold line)
| (325) |
for
![]() , where “
, where “![]() ” is the inner product. This means that all function values
have to
exceed a “tangent” straight line with the subdifferential as slope. As
shown in Figure 137 the
subdifferential at point
” is the inner product. This means that all function values
have to
exceed a “tangent” straight line with the subdifferential as slope. As
shown in Figure 137 the
subdifferential at point ![]() , where the function is continuous
differentiable,
coincides with the derivative. In point
, where the function is continuous
differentiable,
coincides with the derivative. In point ![]() , where the function is
continuous
but not differentiable, the subdifferential consists of all tangent
lines in
between the left and right derivative at that point. Thus, the
subdifferential
in
, where the function is
continuous
but not differentiable, the subdifferential consists of all tangent
lines in
between the left and right derivative at that point. Thus, the
subdifferential
in ![]() is multivalued and a set-valued function. The same applies to the
origin
in Figure 136 (dashed lines). Indeed, by comparing Figures
135 and 136 one observes that the
subdifferential of
the indicator function of
is multivalued and a set-valued function. The same applies to the
origin
in Figure 136 (dashed lines). Indeed, by comparing Figures
135 and 136 one observes that the
subdifferential of
the indicator function of
![]() coincides with
coincides with ![]() :
:
| (326) |
From analysis it is well known that for a continuous differentiable
function a
minimum requires that the derivative is zero. From Figure
137 it
is obvious that for a minimum of a ![]() -continuous function
-continuous function
| (327) |
has to be satisfied. For the indicator function ![]() the definition of
subdifferential reduces to:
the definition of
subdifferential reduces to:
since the indicator function is zero in
![]() .
.
i.e. it is the set of all vectors which make an angle
![]() with
all vectors connecting
with
all vectors connecting
![]() with any other
point
with any other
point
![]() .
.
Looking at Figure 138 the normal cone in ![]() is
is
![]() , in
, in ![]() it is (the vectors on) a straight line locally orthogonal to
it is (the vectors on) a straight line locally orthogonal to
![]() and in
and in ![]() it is (the vectors within)
a cone bordered by the dashed lines. By comparing Equations (328)
and (329) it is clear that:
it is (the vectors within)
a cone bordered by the dashed lines. By comparing Equations (328)
and (329) it is clear that:
| (330) |
This establishes a relationship between the subdifferential and the normal cone concept.
| prox |
(331) |
i.e. it is the point within
![]() which is closest to
which is closest to
![]() . For instance, looking at Figure 138 the
proximal point of
. For instance, looking at Figure 138 the
proximal point of
![]() is
is
![]() and the proximal
point of
and the proximal
point of
![]() is
is
![]() . Now, the concept of
proximal point can be linked to the normal cone and subdifferential
definitions. Indeed:
. Now, the concept of
proximal point can be linked to the normal cone and subdifferential
definitions. Indeed:
| prox |
(332) | ||
| argmin |
(333) | ||
argmin![$\displaystyle _{\{\boldsymbol{x^*} \in
\; \mathcal{C} \} } \left [ \frac{1}{2} \Vert \boldsymbol{x^*} -
\boldsymbol{z} \Vert ^2 \right ]$](img1211.png) |
(334) | ||
argmin![$\displaystyle \left [ \frac{1}{2} \Vert \boldsymbol{x^*} -
\boldsymbol{z} \Vert ^2 + \psi_{\mathcal{C}} (\boldsymbol{x^*}) \right ]$](img1212.png) |
(335) |
Notice that by adding the indicator function the constraint
![]() was removed and a convex constrained
minimization problem is turned into a convex unconstrained minimization
problem. A minimum is obtained if zero belongs to the subdifferential,
i.e.:
was removed and a convex constrained
minimization problem is turned into a convex unconstrained minimization
problem. A minimum is obtained if zero belongs to the subdifferential,
i.e.:
![$\displaystyle \partial \left [ \frac{1}{2} \Vert \boldsymbol{x} -
\boldsymbol{z} \Vert ^2 + \psi_{\mathcal{C}} (\boldsymbol{x}) \right ]$](img1216.png) |
(336) | ||
| (337) | |||
| (338) | |||
| (339) |
This means that one can write:
| (340) |
This finishes the mathematical excursion.
Applying this to the relationship between the gap velocity ![]() and the
normal contact force
and the
normal contact force ![]() one can write:
one can write:
| (341) |
which turns a set relationship into a nonlinear equation, which is easier to solve. Notice that solving for a proximal point usually boils down to a projection on the admissable set.
If friction is present the feasible domain consists of the positive real numbers (including zero) for the normal contact, and a disk with a radius equal to the friction coefficient times the normal force:
| (342) | |||
| (343) | |||
| (344) |
Notice that the feasible domain is split into a normal and a tangential
domain. Therefore, also the projection is split: in normal direction the
projection is on
![]() , in tangential direction on
, in tangential direction on ![]() .
.
In the following a node-to-face contact definition is assumed
(cf. Section 6.7.6) . For the gap
definition one can start from MPC's connecting a slave node with the opposite
master face, e.g. for node ![]() in Figure 139:
in Figure 139:
| (345) |
where
![]() represents the displacement field. In the more general case the coefficients have to be determined from the shape
functions of the master face. The gap vector can now be written as (assuming
the gap is at the beginning of the calculation zero):
represents the displacement field. In the more general case the coefficients have to be determined from the shape
functions of the master face. The gap vector can now be written as (assuming
the gap is at the beginning of the calculation zero):
| (346) |
This vector can be transformed in a
![]() coordinate system
leading to a normal component and two tangential components for the gap. This
can be done for all slave nodes leading to the relationship:
coordinate system
leading to a normal component and two tangential components for the gap. This
can be done for all slave nodes leading to the relationship:
![]() contains the gap in local coordinates. Its length is 3 times the number of
slave nodes in the model (for three-dimensional applications).
contains the gap in local coordinates. Its length is 3 times the number of
slave nodes in the model (for three-dimensional applications). ![]() is
a vector containing the displacements of all contact boundary nodes, i.e. slave
nodes and master nodes, in the global orthogonal coordinate system.
is
a vector containing the displacements of all contact boundary nodes, i.e. slave
nodes and master nodes, in the global orthogonal coordinate system.
![]() represents the initial gap. Assuming small sliding and small
deformations, the matrix
represents the initial gap. Assuming small sliding and small
deformations, the matrix ![]() can be assumed constant. Taking the
derivative w.r.t. time of the above equation yields:
can be assumed constant. Taking the
derivative w.r.t. time of the above equation yields:
where ![]() denotes the velocity of all contact boundary nodes. Now, the equations of motion are written thereby neglecting the mass and
damping terms for the contact boundary nodes (the index i denotes the internal nodes):
denotes the velocity of all contact boundary nodes. Now, the equations of motion are written thereby neglecting the mass and
damping terms for the contact boundary nodes (the index i denotes the internal nodes):
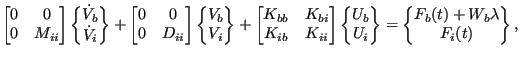 |
(349) |
or
and
Here,
![]() represent the contact forces in the slave nodes in a
local coordinate system. The size of this vector is three times the number of slave
nodes.
represent the contact forces in the slave nodes in a
local coordinate system. The size of this vector is three times the number of slave
nodes.
![]() are the contact forces in all nodes (slave and
master) in global coordinates. The motivation for neglecting the inertia terms
at the contact boundary comes from the fact that these forces were observed
to lead to substantial scatter in the solution in the contact area.
are the contact forces in all nodes (slave and
master) in global coordinates. The motivation for neglecting the inertia terms
at the contact boundary comes from the fact that these forces were observed
to lead to substantial scatter in the solution in the contact area.
From Equation (350) one obtains for
the displacements at the boundary nodes for time increment ![]() :
:
Now, a Verlet scheme in its leapfrog form [69] is proposed based on the
trapezoidal rule and a shifted grid. This means that displacements are
evaluated at times ![]() and
and ![]() , while velocities are evaluated at
times
, while velocities are evaluated at
times
![]() and
and
![]() . Evaluating Equation
(348) at time step
. Evaluating Equation
(348) at time step ![]() and using
and using
![]() one obtains:
one obtains:
![$\displaystyle \{\gamma \}^k = [W_b]^T \frac{(\{U_b\}^k-\{U_b\}^{k-1})}{\Delta t} + \{ \dot{g}_0(t^k) \}.$](img1255.png) |
(353) |
and after substituting ![]() :
:
or, introducing the symmetric matrix ![]() and vector
and vector ![]() :
:
So the contact constraint at time ![]() (also called an inclusion problem):
(also called an inclusion problem):
| (356) |
now amounts to:
or
| (358) |
The latter equation can be solved in an iterative way [102]:
where ![]() is a diagonal matrix with relaxation factors and
is a diagonal matrix with relaxation factors and ![]() is the
iteration index. The relaxation factors are taken to
be
is the
iteration index. The relaxation factors are taken to
be
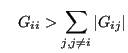 |
(360) | ||
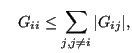 |
(361) |
where
![]() is a relaxation parameter.
is a relaxation parameter.
Summarizing, the contact displacements in time step ![]() are solved using the
following steps (knowing
are solved using the
following steps (knowing
![]() ,
,
![]() ,
, ![]() and
and
![]() ):
):
The solution of the contact problem, however, is restricted to the active
contact degrees of freedom. Indeed, only for the nodes in contact the gap
velocity is positive and Figure 135 applies.
The procedure to determine these active contact degrees of freedom is called an
active set strategy. Two cases are considered. For the initially open case
(i.e. no contact at ![]() ) the gap is calculated at
) the gap is calculated at ![]() by substituting
Equation (352) for
by substituting
Equation (352) for
![]() into Equation (347). The active
degrees of freedom are those for which the gap is nonpositive. For the
preloaded case (i.e. the contact forces at
into Equation (347). The active
degrees of freedom are those for which the gap is nonpositive. For the
preloaded case (i.e. the contact forces at ![]() are positive) the
preload is calculated from Equation (352) assuming sticking contact,
i.e.
are positive) the
preload is calculated from Equation (352) assuming sticking contact,
i.e.
![]() . Then, the active degrees of freedom are those,
for which this sticking contact is changing, i.e. either the normal preload is
negative or the tangential preload exceeds the sticking range and slip
occurs. For details the reader is referred to [69].
. Then, the active degrees of freedom are those,
for which this sticking contact is changing, i.e. either the normal preload is
negative or the tangential preload exceeds the sticking range and slip
occurs. For details the reader is referred to [69].
Once ![]() is calculated
is calculated
![]() can be calculated by
substituting
can be calculated by
substituting
![]() and
and
![]() in
Equation (351) expressed at time
in
Equation (351) expressed at time ![]() leading to:
leading to:
The solution of this set of equations requires a linear equation solver. The mass matrix does not change during the calculation. If the damping matrix
does not change either, the factorization step in the linear equation solver
can be done just once at the start of the calculation. This drastically
reduces the computation time. Knowing
![]() the value of
the displacements in the internal nodes can be obtained from:
the value of
the displacements in the internal nodes can be obtained from:
Consequently, the overall algorithm can be summarized as follows, knowing
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() and
and
![]() :
:
In the first increment (k=1) ![]() ,
,
![]() and
and
![]() have to be known.
have to be known.
Right now, the following limitations apply to the massless contact method: