下一个: Elastic anisotropy with user 上一级: 材料 上一页: The Cailletaud single crystal 目录
This model describes 小变形 for elastically anisotropic materials with a von Mises type yield surface ([24], Section 5.5). Often, this model is used as a compromise for anisotropic materials with lack of data or detailed knowledge about the anisotropic behavior in the viscoplastic range.
It is activated as soon as a *ELASTIC,TYPE=ORTHO card is followed by a *PLASTIC card and/or *CREEP card (the latter without the LAW=USER parameter).
The total strain is supposed to be the sum of the elastic strain and the plastic strain:
| (473) |
An isotropic hardening variable ![]() and a kinematic
hardening tensor
and a kinematic
hardening tensor
![]() are introduced representing the
isotropic and kinematic change of the yield surface,
respectively. The yield surface takes the form:
are introduced representing the
isotropic and kinematic change of the yield surface,
respectively. The yield surface takes the form:
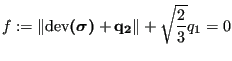 |
(474) |
where
![]() is the deviatoric stress tensor. The constitutive equations for the
hardening variables satisfy:
is the deviatoric stress tensor. The constitutive equations for the
hardening variables satisfy:
| (475) |
and
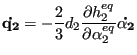 |
(476) |
where ![]() and
and
![]() are the hardening variables
in strain space. It can be shown that
are the hardening variables
in strain space. It can be shown that
| (477) |
| (478) |
where
![]() is the equivalent plastic strain
defined by
is the equivalent plastic strain
defined by
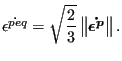 |
(479) |
and
![]() is the equivalent value of the tensor
is the equivalent value of the tensor
![]() defined in a similar way. The isotropic
hardening curve to be defined by the user is
defined in a similar way. The isotropic
hardening curve to be defined by the user is
![]() , the
kinematic one is
, the
kinematic one is
![]() .
.
The constitutive equation for the stress is Hooke's law:
| (480) |
The evolution equations for the plastic strain and the hardening variables in strain space are given by:
| (481) |
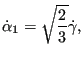 |
(482) |
and
| (483) |
where
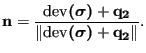 |
(484) |
The variable
![]() is the consistency coefficient known
from the Kuhn-Tucker conditions in optimization theory
[55]. It can be proven to satisfy:
is the consistency coefficient known
from the Kuhn-Tucker conditions in optimization theory
[55]. It can be proven to satisfy:
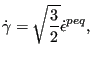 |
(485) |
Finally, the creep rate is modeled as a power law function of the yield exceedance and total time t:
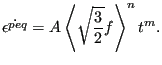 |
(486) |
The brackets
![]() reduce negative function values to zero
while leaving positive values unchanged, i.e.
reduce negative function values to zero
while leaving positive values unchanged, i.e.
![]() if
if ![]() and
and
![]() if
if ![]() .
.
In the present implementation orthotropic elastic behavior is
assumed. Consequently, for each temperature 9
constants need to be defined: ![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,
![]() ,
, ![]() .
.
With isotropic hardening only, the user has to define
![]() underneath the *PLASTIC card, with kinematic hardening only
underneath the *PLASTIC card, with kinematic hardening only
![]() has to be defined underneath a
*PLASTIC, HARDENING=KINEMATIC card. For combined hardening the
has to be defined underneath a
*PLASTIC, HARDENING=KINEMATIC card. For combined hardening the
![]() curve must be defined underneath a *PLASTIC,
HARDENING=KINEMATIC card and
curve must be defined underneath a *PLASTIC,
HARDENING=KINEMATIC card and
![]() underneath a
*CYCLIC HARDENING card. For the viscous constants
the *CREEP card is to be used. So the viscoplastic 输入卡
format is essentially the same as for an elastically isotropic material with
isotropic plasticity.
underneath a
*CYCLIC HARDENING card. For the viscous constants
the *CREEP card is to be used. So the viscoplastic 输入卡
format is essentially the same as for an elastically isotropic material with
isotropic plasticity.
The principal axes of the material are assumed to coincide with the global coordinate system. If this is not the case, use an *ORIENTATION card to define a local system.
For this model, there are 20 internal state variables:
These variables are accessible through the *EL PRINT (.dat file) and *EL FILE (.frd file) keywords in exactly this order (label SDV).
This model is for 小变形 (small strains and small rotations). However, if NLGEOM is activated on the *STEP card this model is considered to be an Abaqus umat routine linking the corotational Cauchy stress to the corotational mechanical 对数应变. In this way, the routine can also be used for large deformations.
Example: *MATERIAL,NAME=MAT1 *ELASTIC,TYPE=ORTHO 500000.,157200.,500000.,157200.,157200.,500000.,126200.,126200., 126200. *CREEP 1.E-10,5,0.
defines a single crystal with elastic constants
500000., 157200., 500000., 157200., 157200., 500000., 126200., 126200.,
126200., and viscoplastic parameters
![]() ,
, ![]() and
and ![]() . The yield surface has a zero radius
and there is no hardening (since neither the *PLASTIC or the *CYCLIC HARDENING
card was used). Only creep is activated.
. The yield surface has a zero radius
and there is no hardening (since neither the *PLASTIC or the *CYCLIC HARDENING
card was used). Only creep is activated.
Example: *MATERIAL,NAME=EL *ELASTIC,TYPE=ORTHO 500000.,157200.,500000.,157200.,157200.,500000.,126200.,126200., 126200. *PLASTIC 100.,0. 110.,0.01 2110.,1.01
defines a single crystal with the same elastic constants as in the previous example. Now, a bilinear isotropic hardening curve is defined. No time dependent behavior was defined.
Example files: anipla, anipla2, anipla3, anipla4, anipla_nl_st,
anipla_nl_dy_imp, anipla_nl_dy_exp.