下一个: 分析类型 上一级: 材料 上一页: 用户弹性各向异性 目录
其他材料定律可以通过 *用户材料 关键字卡片由用户定义。更多信息和示例可在第 节 中找到。
用户材料卡片需要编写用户材料子程序,可以是 CalculiX 类型或 Abaqus 类型。
对于 CalculiX 类型的用户材料子程序,可以参考 umat_user.f 作为示例。输入主要包括增量开始和结束时的机械拉格朗日应变张量,输出是第二类 Piola-Kirchhoff 应力张量以及第二类 Piola-Kirchhoff 应力关于机械拉格朗日应变张量的导数,两者都在增量结束时。其他输入字段的详细信息在上述参考章节中给出。
对于 Abaqus 类型的用户材料子程序,有两种可能性:要么用户只想将子程序应用于线性几何计算。在这种情况下,进入或离开子程序的应变和应力类型并不重要,前一段内容适用。但是,如果用户想将子程序应用于几何非线性计算,进入子程序的是共旋机械对数应变,所需应力是共旋柯西应力。因此,CalculiX 在调用 Abaqus 用户材料子程序之前和之后必须执行一些转换。Abaqus 用户材料子程序的原型示例请参考 umat.f,关于 Abaqus 接口字段使用的限制请参阅第 节。
这里给出一些关于 CalculiX 中使用的场(机械拉格朗日应变和第二类 Piola-Kirchhoff 应力)如何转换为 Abaqus 所需场(共旋机械对数应变和共旋柯西应力)以及反向转换的信息。转换代码在 umat_abaqusnl.f 中。场
![]() 、
、
![]() 和
和
![]() 在子程序开始时可用(这些变量的含义在以下段落中解释)。
在子程序开始时可用(这些变量的含义在以下段落中解释)。
机械对数应变满足:
| SB|(487) |
其中
![]() 是机械变形梯度
是机械变形梯度
![]() 的特征值。在 CalculiX 中,机械变形梯度是通过从总变形梯度中减去热膨胀得到的,即:
的特征值。在 CalculiX 中,机械变形梯度是通过从总变形梯度中减去热膨胀得到的,即:
| TT|(488) |
对于各向同性膨胀。这是将总变形梯度分解为机械分量和热分量的乘积分解的一阶近似,形式为
![]() ,另请参见
,另请参见
![]() 。旋转张量
。旋转张量
![]() 将物质坐标中运动的主向量
将物质坐标中运动的主向量
![]() 旋转到空间坐标
旋转到空间坐标
![]() :
:
| QM|(489) |
它是一个二点张量,一只脚在物质参考系中,另一只脚在空间参考系中。共旋机械对数应变然后等于(回忆
![]() 是正交的,即
是正交的,即
![]() ):
):
| PP|(490) |
![]() 可以从机械拉格朗日张量
可以从机械拉格朗日张量
![]() 的特征值得到,其特征向量为
的特征值得到,其特征向量为
![]() 。
。
柯西张量满足:
| MQ|(491) |
因此共旋柯西张量等于:
| MN|(492) |
这里,![]() 是雅可比行列式,
是雅可比行列式,
![]() 是第二类 Piola-Kirchhoff 应力,
是第二类 Piola-Kirchhoff 应力,
![]() 是右伸缩张量。后者是柯西-格林张量
是右伸缩张量。后者是柯西-格林张量
![]() 的平方根,因此它也可以从拉格朗日张量推导。然而,在 umat_abaqusnl.f 子程序中,机械拉格朗日张量是可用的,而总张量不可用。因此,需要总右伸缩张量和机械右伸缩张量之间的关系。由于
的平方根,因此它也可以从拉格朗日张量推导。然而,在 umat_abaqusnl.f 子程序中,机械拉格朗日张量是可用的,而总张量不可用。因此,需要总右伸缩张量和机械右伸缩张量之间的关系。由于
![]() 与
与
![]() 具有相同的特征值,变形梯度的乘积分解为机械和热变形梯度导致
具有相同的特征值,变形梯度的乘积分解为机械和热变形梯度导致
![]() ,可得:
,可得:
| SX|(493) |
后者方程假设热膨胀是各向同性的。在 umat_abaqusnl.f 子程序中,
![]() 是已知的,
是已知的,
![]() 可以从
可以从
![]() 获得,
获得,
![]() 来自:
来自:
 |
RN|(494) |
其中下标
![]() 指相应矩阵的元素 (1,1)。通过这种方式,共旋柯西应力从第二类 Piola-Kirchhoff 应力获得。从 Abaqus 材料用户子程序返回后使用逆关系:
指相应矩阵的元素 (1,1)。通过这种方式,共旋柯西应力从第二类 Piola-Kirchhoff 应力获得。从 Abaqus 材料用户子程序返回后使用逆关系:
| HK|(495) |
现在,CalculiX 需要
![]() (即总拉格朗日方法),然而,Abaqus 子程序返回
(即总拉格朗日方法),然而,Abaqus 子程序返回
![]() 。现在,考虑到以下因素:
。现在,考虑到以下因素:
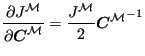 |
NV|(496) |
并在直角坐标系中写出第二类 Piola-Kirchhoff 应力的表达式:
| QB|(497) |
直接求导得:
| XY| | ||
| NT| | 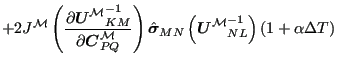 |
XY| |
| NT| |  |
XY| |
| NT| | 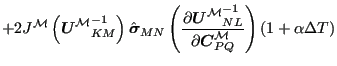 |
YX|(498) |
第二行括号中的第一项,第三行括号中的第三项和第四行括号中的第二项是函数关于
![]() 对
对
![]() 求导的特殊情况。基于
求导的特殊情况。基于
![]() 的特征值和结构张量的此类求导表达式由 Itskov [42]
推导并汇总在 [25] 的附录中。第三行括号中的第二项是 Abaqus UMAT 子程序返回的切线。
的特征值和结构张量的此类求导表达式由 Itskov [42]
推导并汇总在 [25] 的附录中。第三行括号中的第二项是 Abaqus UMAT 子程序返回的切线。
请注意,上述方程在 (KL) 和 (PQ) 中是对称的,即交换 K 和 L 和/或 P 和 Q。特别是,在第二项中交换 K 和 L 导致第四项。这种对称性是预期的,因为
![]() 和
和
![]() 是对称张量。然而,目前尚不清楚用 PQ 替换 KL 获得的对称性是否被保留。因此,在 CalculiX 中对生成的切线矩阵进行对称化处理,得到 21 个常数而不是 36 个。上述过程在 umat_abaqusnl.f 和 umat_abaqusnl_total.f 中实现。它仅用于那些仅为小应变 formul 的材料模型,例如弹塑性正交各向异性的等向塑性、Johnson_Cook 塑性和 Mohr_Coulomb 塑性。
是对称张量。然而,目前尚不清楚用 PQ 替换 KL 获得的对称性是否被保留。因此,在 CalculiX 中对生成的切线矩阵进行对称化处理,得到 21 个常数而不是 36 个。上述过程在 umat_abaqusnl.f 和 umat_abaqusnl_total.f 中实现。它仅用于那些仅为小应变 formul 的材料模型,例如弹塑性正交各向异性的等向塑性、Johnson_Cook 塑性和 Mohr_Coulomb 塑性。