Next: Three-dimensional Navier-Stokes Calculations Up: Types of analysis Previous: Hydraulic Networks Contents
The turbulent flow in open channels can be approximated by one-dimensional network calculations. For the theoretical background the reader is referred to [17] and expecially [12] (in Dutch). [22] contains information on the solution of transient problems and (transient and steady state) analytical examples. The governing equation is the Bresse equation, which is a special form of the Bernoulli equation. For its derivation we start from Equation (613), which we write down for a flow line near the bottom of the channel in the form:
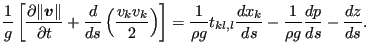 |
(621) |
Assuming:
one arrives at:
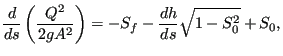 |
(622) |
where (Figure 147) h is the water depth (measured perpendicular to the channel floor), s is the
length along the bottom,
![]() , where
, where ![]() is the angle the
channel floor makes with a horizontal line,
is the angle the
channel floor makes with a horizontal line, ![]() is a friction term (head
loss per unit of length; results from the viscous stresses),
is a friction term (head
loss per unit of length; results from the viscous stresses), ![]() is
the earth acceleration,
is
the earth acceleration, ![]() is the volumetric flow (mass flow divided by the
fluid density) and
is the volumetric flow (mass flow divided by the
fluid density) and ![]() is the area of the cross section. This also amounts to:
is the area of the cross section. This also amounts to:
![$\displaystyle \frac{Q}{gA^2} \frac{dQ}{ds} - \frac{Q^2}{gA^3} \left [ \left . \...
...}{\partial h} \frac{dh}{ds} \right ] + \frac{dh}{ds} \sqrt{1-S_0^2} = S_0 -S_f.$](img1923.png) |
(623) |
Assuming no change in flow (dQ/ds=0) and a trapezoidal cross section (for which
![]() , where
, where ![]() is the width at the free surface) one
finally obtains (Bresse equation):
is the width at the free surface) one
finally obtains (Bresse equation):
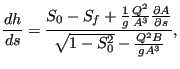 |
(624) |
For ![]() several formulas have been
proposed. In CalculiX the White-Colebrook and the Manning formula are
implemented. The White-Colebrook formula reads
several formulas have been
proposed. In CalculiX the White-Colebrook and the Manning formula are
implemented. The White-Colebrook formula reads
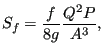 |
(625) |
where ![]() is the friction coefficient determined by Equation
(163), and
is the friction coefficient determined by Equation
(163), and ![]() is the wetted circumference of the cross
section. The Manning formula reads
is the wetted circumference of the cross
section. The Manning formula reads
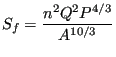 |
(626) |
where ![]() is the Manning coefficient, which has to be determined
experimentally.
is the Manning coefficient, which has to be determined
experimentally.
In CalculiX, the channel cross section has to be trapezoidal (Figure 147). For this geometry the following relations apply:
| (627) |
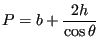 |
(628) |
and
| (629) |
All geometry parameters are assumed not to change within an
element(allowing a changing geometry within an element leads to complications,
e.g. a non-constant width ![]() may lead to a fall (i.e. a transition from
subcritical flow to supercritical flow) within one and the same element. In
CalculiX. a changing width can be treated in a discontinuous way by using the
Contraction element). Consequently:
may lead to a fall (i.e. a transition from
subcritical flow to supercritical flow) within one and the same element. In
CalculiX. a changing width can be treated in a discontinuous way by using the
Contraction element). Consequently:
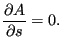 |
(630) |
and one obtains the Bresse equation in the form (for White-Colebrook):
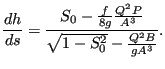 |
(631) |
Recall that in the above formula ![]() ,
, ![]() and
and ![]() are a function of the depth
are a function of the depth
![]() . The numerator has for positive
. The numerator has for positive ![]() exactly one root, which is called the normal depth. For
this depth there is no change in
exactly one root, which is called the normal depth. For
this depth there is no change in ![]() along the channel. For zero or negative
along the channel. For zero or negative
![]() there is no root. The denominator
has always exactly one root, called the critical depth. For this depth the slope is
infinite. It is very weakly dependent on
there is no root. The denominator
has always exactly one root, called the critical depth. For this depth the slope is
infinite. It is very weakly dependent on ![]() . Notice that both the normal
depth (if defined) and the critical depth are monotonically increasing
functions of the volumetric fluid flow.
. Notice that both the normal
depth (if defined) and the critical depth are monotonically increasing
functions of the volumetric fluid flow.
Let us for the time being assume that ![]() is positive. For
is positive. For ![]() close to zero
both the denominator and numerator are negative, so the slope of
close to zero
both the denominator and numerator are negative, so the slope of ![]() is
positive. For high enough values of
is
positive. For high enough values of ![]() both are positive, which also leads to
a positive slope for
both are positive, which also leads to
a positive slope for ![]() . Only for values of
. Only for values of ![]() in between the normal and critical
depth the slope
in between the normal and critical
depth the slope ![]() is negative. For low values of
is negative. For low values of ![]() the normal depth
exceeds the critical depth and the corresopnding channel slope (slope of the
bottom) is called weak. The corresponding water curves are denoted by A1, A2 and A3 depending on whether the curve is above
the normal depth, in between normal depth and critical depth or below the
critical depth, respectively. For high values of
the normal depth
exceeds the critical depth and the corresopnding channel slope (slope of the
bottom) is called weak. The corresponding water curves are denoted by A1, A2 and A3 depending on whether the curve is above
the normal depth, in between normal depth and critical depth or below the
critical depth, respectively. For high values of ![]() the critical
depth exceeds the normal depth and the corresponding channel slope is called
strong. The corresponding water curves are denoted by B1, B2 and B3 depending on whether the curve is above the critical
depth, in between the critical depth and the normal depth or below the normal
depth, respectively. Water curves below the critical depth are governed by
upstream boundary conditions and are called frontwater curves. Water curves
above the critical depth are governed by downstream boundary conditions and
are called backwater curves.
the critical
depth exceeds the normal depth and the corresponding channel slope is called
strong. The corresponding water curves are denoted by B1, B2 and B3 depending on whether the curve is above the critical
depth, in between the critical depth and the normal depth or below the normal
depth, respectively. Water curves below the critical depth are governed by
upstream boundary conditions and are called frontwater curves. Water curves
above the critical depth are governed by downstream boundary conditions and
are called backwater curves.
Channel flow can be supercritical or subcritical. For supercritical flow the
velocity exceeds the propagation speed ![]() of a wave, which satisfies
of a wave, which satisfies
![]() . Defining the Froude number by
. Defining the Froude number by ![]() , where U is the velocity of the
fluid, supercritical flow corresponds to
, where U is the velocity of the
fluid, supercritical flow corresponds to ![]() . Supercritical flow is
controlled by upstream boundary conditions. If the flow is subcritical
(
. Supercritical flow is
controlled by upstream boundary conditions. If the flow is subcritical
(![]() ) it is controlled by downstream boundary conditions. In a subcritical
flow disturbances propagate upstream and downstream, in a supercritical flow
they propagation downstream only. The critical depth corresponds to
) it is controlled by downstream boundary conditions. In a subcritical
flow disturbances propagate upstream and downstream, in a supercritical flow
they propagation downstream only. The critical depth corresponds to
![]() . Indeed, taking a rectangular cross section the denominator of the
Bresse equation is zero if
. Indeed, taking a rectangular cross section the denominator of the
Bresse equation is zero if
| (632) |
For frontwater curves ![]() is less than the critical depth, consequently the
velocity must exceed
is less than the critical depth, consequently the
velocity must exceed ![]() (conservation of mass) and is supercritical. For
backwater curves
(conservation of mass) and is supercritical. For
backwater curves ![]() exceeds the critical depth and the velocity is less than
exceeds the critical depth and the velocity is less than
![]() , the flow is subcritical.
, the flow is subcritical.
A transition from supercritical to subcritical flow is called a hydraulic jump, a transition from subcritical to supercritical flow is a fall. At a jump the following equation is satisfied [17]:
| (633) |
where ![]() are the cross sections before and after the jump,
are the cross sections before and after the jump,
![]() and
and ![]() is the distance orthogonal to the channel floor
between the fluid surface and the center of gravity of section
is the distance orthogonal to the channel floor
between the fluid surface and the center of gravity of section ![]() and
and
![]() , respectively,
, respectively, ![]() is
the fluid density and
is
the fluid density and ![]() is the mass flow. This relationship can be
obtained by applying the conservation of momentum principle to a mass of
infinitesimal width at the jump. The conservation of momentum dictates that
the time rate of change of the momentum must equal all external forces. In
Figure 148 a mass of width
is the mass flow. This relationship can be
obtained by applying the conservation of momentum principle to a mass of
infinitesimal width at the jump. The conservation of momentum dictates that
the time rate of change of the momentum must equal all external forces. In
Figure 148 a mass of width ![]() is shown at time
is shown at time ![]() crossing a jump. At time
crossing a jump. At time
![]() this mass is moved to the right (width
this mass is moved to the right (width ![]() ). The change in momentum in s-direction
amounts to
). The change in momentum in s-direction
amounts to
| (634) |
The forces are the hydrostatic forces on the right and left side of the mass:
| (635) |
All other forces such as gravity and wall friction disappear for
![]() . Equating both terms yields the jump equation. Notice that this
relationship cannot be obtained by using the Bresse equation, since
. Equating both terms yields the jump equation. Notice that this
relationship cannot be obtained by using the Bresse equation, since ![]() is
discontinuous at the jump. The discrete form of the
Bernoulli equation (615) cannot be used either, since it
is obtained by integrating the differential form and
is
discontinuous at the jump. The discrete form of the
Bernoulli equation (615) cannot be used either, since it
is obtained by integrating the differential form and
![]() is
discontinuous. However, one can write down Equation
(615) pro forma and deduce the head loss in a jump by
formally substituting the jump equation. One obtains:
is
discontinuous. However, one can write down Equation
(615) pro forma and deduce the head loss in a jump by
formally substituting the jump equation. One obtains:
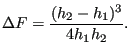 |
(636) |
Since the head loss must
be positive, this also proves that a fall cannot occur in a prismatic channel
(i.e. a channel with constant cross section). Therefore, a fall can only occur at discontinuities in the
channel geometry, e.g. at a discontinuous increase of the channel floor
slope ![]() .
.
This approach opens up an alternative to using the conservation of momentum principle at discontinuities: if one knows the head loss (e.g. by performing experiments) one can apply the discrete form of the Bernoulli equation in the form:
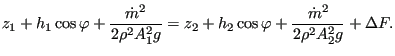 |
(637) |
Defining the specific energy ![]() by:
by:
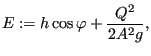 |
(638) |
one can write the above equation as
![]() , from
which it is clear that the total head
, from
which it is clear that the total head ![]() can never increase in the direction of the flow,
however, the specific energy can. From the definition of the specific energy
one can derive the dependence of
can never increase in the direction of the flow,
however, the specific energy can. From the definition of the specific energy
one can derive the dependence of ![]() on
on ![]() , as shown in Figure
149:
, as shown in Figure
149:
To determine the maximum allowable volumetric flow for a given value of ![]() one has to set the first derivative of the above equation to zero, resulting
in (recall that
one has to set the first derivative of the above equation to zero, resulting
in (recall that
![]() ):
):
| (640) |
Substituting this expression in Equation (639) yields:
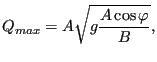 |
(641) |
or
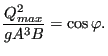 |
(642) |
This corresponds to the denominator of the Bresse equation, i.e. the depth for
which the volumetric flow is maximum is the critical depth. This is
illustrated in Figure 149. Curves corresponding to lower
values of ![]() also go through the origin and are completely contained in the
curve shown. These curves cannot intersect, since this would mean that the
intersection point corresponds to different energy values.
also go through the origin and are completely contained in the
curve shown. These curves cannot intersect, since this would mean that the
intersection point corresponds to different energy values.
For a volumetric flow lower than the maximal one (![]() in the figure), two depths are feasible: a
subcritical one and a supercritical one. The transition from a supercritical
one to a subcritical corresponds to a jump. At the location of the jump
in the figure), two depths are feasible: a
subcritical one and a supercritical one. The transition from a supercritical
one to a subcritical corresponds to a jump. At the location of the jump
![]() , however,
, however,
![]() , so
, so ![]() and the subcritical
height will be slightly lower than in the figure. For geometric
discontinuities for which the head loss is known (e.g. for a contraction or an
enlargement) the above reasoning can be used to obtain the fluid depth
downstream of the discontinuity based on the specific energy upstream (or vice versa).
and the subcritical
height will be slightly lower than in the figure. For geometric
discontinuities for which the head loss is known (e.g. for a contraction or an
enlargement) the above reasoning can be used to obtain the fluid depth
downstream of the discontinuity based on the specific energy upstream (or vice versa).
Available boundary conditions for channels are the sluice gate and the weir (upstream conditions) and the infinite reservoir (downstream condition). They are described in Section 6.6. Discontinuous changes within a channel can be described using the contraction, enlargement and step elements.
The elements used in CalculiX for one-dimensional channel networks are regular network elements, in which the unknowns are the fluid depth (in z-direction, i.e. not orthogonal to the channel floor) and the temperature at the end nodes and the mass flow in the middle nodes. The equations at our disposal are the Bresse equation in the middle nodes (conservation of momentum), and the mass and energy conservation (Equations 609 and 618, respectively) at the end nodes.
For channel elements the energy equation is used in its original form:
in which ![]() for the incoming flow is determined at the correct upstream
temperature
for the incoming flow is determined at the correct upstream
temperature ![]() .
. ![]() is the temperature of the wall. The temperatures in the network are solved for as
soon as the mass flow and fluid depth have been determined in the complete
network. The above equation is applied on an element by element basis starting
at the upstream In/Out elements and going in downstream direction. It can be reformulated as:
is the temperature of the wall. The temperatures in the network are solved for as
soon as the mass flow and fluid depth have been determined in the complete
network. The above equation is applied on an element by element basis starting
at the upstream In/Out elements and going in downstream direction. It can be reformulated as:
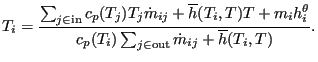 |
(644) |
This is a slightly nonlinear equation in ![]() which is solved node by node in
an iterative way. Convection with the wall can be
defined using a *FILM card (forced convection), for the heat
source *CFLUX is to be used on degree of freedom 0 (or,
equivalently, 11).
which is solved node by node in
an iterative way. Convection with the wall can be
defined using a *FILM card (forced convection), for the heat
source *CFLUX is to be used on degree of freedom 0 (or,
equivalently, 11).
Radiation to the environment can be included by modifying Equation (643) into:
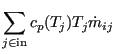 |
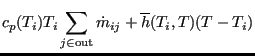 |
||
| (645) |
where ![]() is the representative radiating surface for
is the representative radiating surface for ![]() ,
, ![]() is the
emissivity,
is the
emissivity, ![]() is the Stefan-Boltzmann constant and all temperatures
have to be on an absolute scale. The radiating surface can be modeled using
shell elements or solid elements covering the fluid surface. The above
equation is a quartic equation, which can be solved using the conventional
Newton-Raphson technique. Due to the independent processing of the energy equation
after having solved the mass and momentum equation it is assumed that a change
in
temperature does not significantly influence the flow conditions.
is the Stefan-Boltzmann constant and all temperatures
have to be on an absolute scale. The radiating surface can be modeled using
shell elements or solid elements covering the fluid surface. The above
equation is a quartic equation, which can be solved using the conventional
Newton-Raphson technique. Due to the independent processing of the energy equation
after having solved the mass and momentum equation it is assumed that a change
in
temperature does not significantly influence the flow conditions.
Output variables are the mass flow (key MF on the *NODE
PRINT or *NODE
FILE card), the fluid depth (key PN -- network pressure -- on the *NODE
PRINT card and DEPT on the *NODE
FILE card) and the total temperature
(key NT on the *NODE
PRINT card and TT on the *NODE
FILE card). These are the primary variables in the
network. Internally, in network nodes,
components one to three of the structural displacement field are used for the
mass flow, the fluid depth and the critical depth, respectively. So their
output can also be obtained by requesting
U on the *NODE PRINT card. This is the only way to get the
critical depth in the .dat file. In the .frd file the critical depth can be
obtained by selecting HCRI on the *NODE
FILE card. Notice that for liquids the total temperature virtually coincides
with the static temperature (cf. previous section; recall that the wave speed in a channel
with water depth 1 m is ![]() m/s). If a jump occurs in the network,
this is reported on the screen listing the element in which the jump takes
place and its relative location within the element.
m/s). If a jump occurs in the network,
this is reported on the screen listing the element in which the jump takes
place and its relative location within the element.