Shallow water calculations

Calculations for incompressible fluids with a free surface are quite important in marine and oceanographic applications. The challenging part here is to predict the location of the free surface. A special subcategory are the problems in which the depth of the fluid is small compared to the other dimensions. In that case the general equations can be reduced to the so-called shallow water equations. These equations have a very similar behavior as the Navier-Stokes equations for compressible fluids, treated in the previous section. Linearization of these equations leads to the linear shallow water equations treated in Section 6.9.10.

Starting point for the derivation of the shallow water equations are the conservation of mass and momentum for incompressible fluids:

$$v_{i,i}=0$$ (706)

and

$$\frac{\partial v_j}{\partial t} + \frac{\partial }{\partial x_i} ... ...\partial x_j} - \frac{1}{\rho } \frac{\partial t_{ij}}{\partial x_i} - f_j = 0.$$ (707)

Now, the depth-direction of the fluid is assumed to coincide with the $x_3$-direction. The momentum equation in the $x_3$-direction now reads:

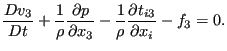$$\frac{D v_3}{D t} + \frac{1}{\rho } \frac{\partial p}{\partial x_3} - \frac{1}{\rho } \frac{\partial t_{i3}}{\partial x_i} - f_3 = 0.$$ (708)

The velocity in depth direction (first term) is assumed to be neglegible as well as the viscous stress components $t_{i3}$. Furthermore, the volumetric force density is assumed to reduce to the gravity $g$. Consequently, one obtains:

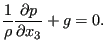$$\frac{1}{\rho } \frac{\partial p}{\partial x_3} + g =0.$$ (709)

Now, the depth is supposed to be composed of two contributions: a portion $H$ extending from $x_3=-H$ ($H>0$) up to $x_3=0$, and a portion $\eta$ extending from $x_3=0$ up to $x_3=\eta$ ( $-\infty < \eta < \infty$), so that the depth h amounts to $h=H+\eta$ (Figure ...). Integrating the above equation and applying the boundary condition $p=p_a$ for $x_3=\eta$, where $p_a$ is the atmospheric pressure, one obtains:

$$p=\rho g (\eta -x_3) + p_a,$$ (710)

expressing the the pressure increases linearly from the surface into the depth direction.

The conservation of mass equation can be integrated in z-direction as follows:

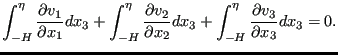$$\int_{-H}^{\eta } \frac{\partial v_1}{\partial x_1} dx_3 + \int_{... ...rtial x_2} dx_3 + \int_{-H}^{\eta } \frac{\partial v_3}{\partial x_3} dx_3 = 0.$$ (711)

Applying the Leibniz rule to the first two equations and direct integration to the last term leads to:

$$\frac{\partial }{\partial x_1} \left( \int_{-H}^{\eta } v_1 dx_3 ... ...) \frac{\partial \eta }{\partial x_1} - v_1(-H) \frac{\partial H}{\partial x_1}$$

$$+\frac{\partial }{\partial x_2} \left( \int_{-H}^{\eta } v_2 dx_3... ...) \frac{\partial \eta }{\partial x_2} - v_2(-H) \frac{\partial H}{\partial x_2}$$

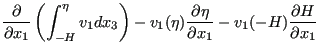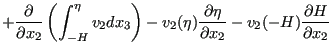$$+ v_3(\eta) - v_3(-H) =0.$$ (712)

The velocity at the bottom is zero, i.e. $v_1(-H)=v_2(-H)=v_3(-H)=0$. Furthermore, a mean velocity is now defined by:

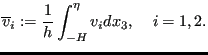$$\overline{v}_i := \frac{1}{h} \int_{-H}^{\eta } v_i dx_3, \;\;\;\; i=1,2.$$ (713)

This leads to:

$$\frac{\partial }{\partial x_1} \left( \overline{v}_1 h \right) - v_1(\eta) \frac{\partial \eta }{\partial x_1}$$

$$+\frac{\partial }{\partial x_2} \left(\overline{v}_2 h \right) - v_2(\eta) \frac{\partial \eta }{\partial x_2}$$

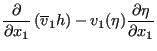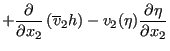$$+ v_3(\eta) =0.$$ (714)

Now, the vertical velocity at the free surface can be written as:

$$v_3(\eta ) := \frac{D \eta }{dt } = \frac{\partial \eta }{\partia... ...ta }{\partial x_1} v_1(\eta ) + \frac{\partial \eta }{\partial x_2} v_2(\eta ),$$ (715)

leading to:

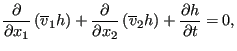$$\frac{\partial }{\partial x_1} \left( \overline{v}_1 h \right) +\... ...partial x_2} \left(\overline{v}_2 h \right) + \frac{\partial h}{\partial t} =0,$$ (716)

since $\partial H/\partial t=0$. With $\overline{v_3}=0$ one can also write:

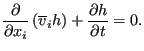$$\frac{\partial }{\partial x_i} \left( \overline{v}_i h \right) + \frac{\partial h}{\partial t} =0.$$ (717)

This is identical to Equation 676 (conservation of mass for a compressible fluid) in which $v_i$ is replaced by $\overline{v_i}$ and $\rho$ by $h$.

Integrating the momentum equation, i.e. Equation (707) in $x_1$ and $x_2$ direction across the depth leads to:

$$\frac{\partial }{\partial t} ( \overline{u_i} h) - v_i (\eta)\fra... ... + \sum_{j=1}^{2} \frac{\partial }{\partial x_j} \int_{-H}^{\eta } v_i v_j dx_3$$

$$- \sum_{j=1}^{2} v_i (\eta) v_j (\eta ) \frac{\partial \eta }{\pa... ..._{j=1}^{2} v_i(-H) v_j(-H) \frac{\partial H}{\partial x_j} + v_i(\eta)v_3(\eta)$$

$$- v_i(-H)v_3(-H) + \frac{1}{\rho } \int_{-H}^{\eta } \frac{\parti... ...H}^{\eta } \frac{\partial t_{ij}}{\partial x_j} - \frac{1}{\rho } t_{i3} (\eta)$$

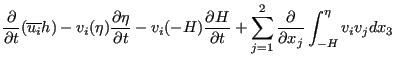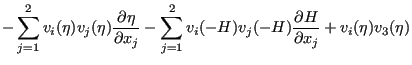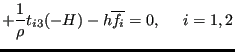$$+ \frac{1}{\rho } t_{i3} (-H) - h \overline{f_i} =0 , \;\;\;\;\; i=1,2$$ (718)

Since the velocity at the bottom is zero, the third, sixth and eight term vanish. Due to the definition of the vertical velocity at the free surface, Equation (715) the second, fifth and seventh term also disappear. Due to Equation (710) the ninth term amounts to:

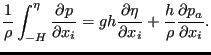$$\frac{1}{\rho } \int_{-H}^{\eta } \frac{\partial p}{\partial x_i}... ...rtial \eta }{\partial x_i} + \frac{h}{\rho } \frac{\partial p_a}{\partial x_i}.$$ (719)

The fourth term is approximated by:

$$\sum_{j=1}^{2} \frac{\partial }{\partial x_j} \int_{-H}^{\eta } v_i v_j dx_3 = \sum_{j=1}^{2} \frac{\partial }{\partial x_j} \left ( h \overli... ...v}_j + \int_{-H}^{\eta } \langle v \rangle_i \langle v \rangle _j \right ) dx_3$$

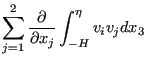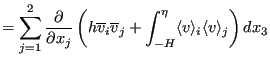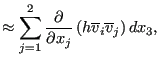$$\approx \sum_{j=1}^{2} \frac{\partial }{\partial x_j} \left ( h \overline{v}_i \overline{v}_j \right ) dx_3,$$ (720)

and the tenth term is neglected. This leads to:

$$\frac{\partial }{\partial t} (h \overline{u}_i ) + \sum_{j=1}^{2} \frac{\partial }{\partial x_j} h \overline{v}_i \overline{v}_j = - g h \frac{\partial \eta }{\partial x_i} - \frac{h}{\rho } \frac{\partial p_a}{\partial x_i} + \frac{1}{\rho } t_{i3}^s$$

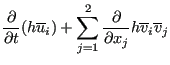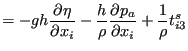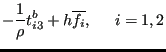$$- \frac{1}{\rho } t_{i3}^b + h \overline{f_i} , \;\;\;\;\; i=1,2$$ (721)

Now, $h \partial \eta / \partial x_i$ can also be written as:

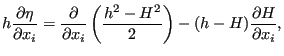$$h \frac{\partial \eta }{\partial x_i} = \frac{\partial }{\partial x_i} \left( \frac{h^2 -H^2}{2} \right) - (h-H) \frac{\partial H}{\partial x_i},$$ (722)

leading to:

$$\frac{\partial }{\partial t} (h \overline{u}_i ) + \sum_{j=1}^{2} \frac{\partial }{\partial x_j} h \overline{v}_i \overline{v}_j = - \frac{\partial \overline{p} }{\partial x_i} + g(h-H) \frac{\partial H}{\partial x_i} - \frac{h}{\rho } \frac{\partial p_a}{\partial x_i}$$

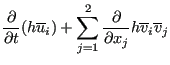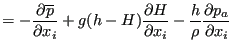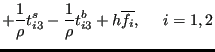$$+ \frac{1}{\rho } t_{i3}^s - \frac{1}{\rho } t_{i3}^b + h \overline{f_i} , \;\;\;\;\; i=1,2$$ (723)

were an artifical pressure $\overline{p}$ has been defined by:

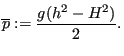$$\overline{p} := \frac{g(h^2 -H^2)}{2}.$$ (724)

Since there is no variation in depth direction and setting $t_{33}^s=t_{33}^b=f_3=0$ this also amounts to:

$$\frac{\partial }{\partial t} (h \overline{u}_i ) + \frac{\partial }{\partial x_j} h \overline{v}_i \overline{v}_j = - \frac{\partial \overline{p} }{\partial x_i} + g(h-H) \frac{\partial H}{\partial x_i} - \frac{h}{\rho } \frac{\partial p_a}{\partial x_i}$$

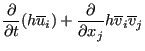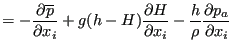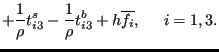$$+ \frac{1}{\rho } t_{i3}^s - \frac{1}{\rho } t_{i3}^b + h \overline{f_i} , \;\;\;\;\; i=1,3.$$ (725)

This amounts to the conservation of momentum equation (672) for a compressible fluid with the density $\rho$ replaced by $h$, $v_i$ replaced by $\overline{v}_i$, $p$ replaced by $\overline{p}$, $t_{ik}$ neglected and $\rho g_i$ replaced by

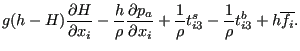$$g(h-H) \frac{\partial H}{\partial x_i} - \frac{h}{\rho } \frac{\p... ... x_i} + \frac{1}{\rho } t_{i3}^s - \frac{1}{\rho } t_{i3}^b + h \overline{f_i}.$$ (726)

The friction stress at the bottom is frequently modeled by a hydraulic resistance type formula such as

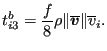$$t_{i3}^b = \frac{f}{8} \rho \Vert \boldsymbol{\overline{v} } \Vert \overline{v}_i.$$ (727)

The energy equation can be integrated in a similar way. I can be used of some fluid at a higher temperature is released into the flow and one would like to study the spread of the heat. The equation for incompressible flow runs:

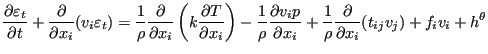$$\frac{\partial \varepsilon_t}{\partial t} + \frac{\partial }{\par... ...{1}{\rho } \frac{\partial }{\partial x_i} ( t_{ij} v_j) + f_i v_i + h^{\theta }$$ (728)

Integrating from -H to $\eta$ yields:

$$\frac{\partial }{\partial t} \int_{-H}^{\eta } \varepsilon_t dx_3... ...artial t} \varepsilon_t(\eta) - \frac{\partial H}{\partial t} \varepsilon_t(-H)$$

$$+ \sum_{i=1}^{2} \frac{\partial }{\partial x_i} \int_{-H}^{\eta }... ...} \frac{\partial H}{\partial x_i} \left . (v_i \varepsilon_t) \right\vert _{-H}$$

$$+ \left . (v_3 \varepsilon_t) \right\vert _{\eta } - \left . (v_3... ...\partial }{\partial x_i} \left ( k \frac{\partial T}{\partial x_i} \right) dx_3$$

$$- \frac{1}{\rho } (q^s + q^b) - \sum_{i=1}^{3} \frac{1}{\rho } \i... ...ac{1}{\rho } \int_{-H}^{\eta} \frac{\partial }{\partial x_i} ( t_{ij} v_j) dx_3$$

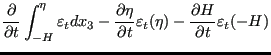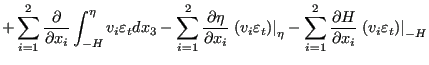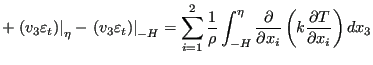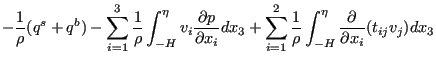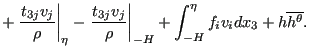$$+ \left . \frac{t_{3j}v_j}{\rho } \right\vert _{\eta} - \left . \... ... \right\vert _{-H} + \int_{-H}^{\eta} f_i v_i dx_3 + h \overline{h^{\theta }} .$$ (729)

Terms 3, 6 and 8 on the left hand side and term 6 on the right hand side are zero (no velocity at the bottom and no change in time of the bottom level). Terms 2, 5 and 7 on the left hand side disappear due to Equation (715). The integral in the first term on left hand side is replaced by definition by $\overline{\varepsilon_t} h$ and the integral in the fourth term is approximated by $\overline{v}_i \overline{\varepsilon_t} h$. The variables $q^s$ and $q^b$ in the second term on the right hand side are the heat flux flowing out of the fluid at the surface and the bottom, respecitively.

Substituting the expression for the pressure, i.e. Equation (710) into the third term on the right hand side yields (the summation in that term really only extends from 1 to 2 since $v_3$ is neglegible):

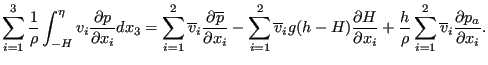$$\sum_{i=1}^{3} \frac{1}{\rho } \int_{-H}^{\eta} v_i \frac{\partia... ...frac{h}{\rho } \sum_{i=1}^{2} \overline{v}_i \frac{\partial p_a}{\partial x_i}.$$ (730)

The first and the fourth term on the right hand side is neglected and the eighth term is approximated by $\overline{f}_i \overline{v}_i h$. This finally yields:

$$\frac{\partial }{\partial t} (h \overline{\varepsilon_t}) + \frac... ...t [ (h \overline{\varepsilon_t} + \overline{p}) \overline{v}_i \right ] \approx - \frac{1}{\rho } (q^s + q^b) + \overline{v}_i g(h-H) \frac{\part... ...partial x_i} - \frac{h}{\rho } \frac{\partial p_a}{\partial x_i} \overline{v}_i$$

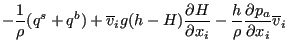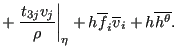$$+ \left . \frac{t_{3j}v_j}{\rho } \right\vert _{\eta} + h \overline{f}_i \overline{v}_i + h \overline{h^{\theta }}.$$ (731)

This is equivalent to the energy equation for compressible fluids with $\rho$ replaced by $h$ and appropriate source terms. The neglection of the stress and conduction terms (except in $x_3$-direction) can be obtained by setting $\mu=\lambda=0$. No specific gas constant has to be defined. The parameter COMPRESSIBLE on the *CFD card has to be replaced by the SHALLOW WATER parameter. The pressure initial and boundary conditions have to be replaced by conditions for $\overline{p}=g(h^2-H^2)/2$. If $H$ corresponds to the fluid surface in rest, the initial conditions ususally reduce to $\overline{p}=0$.