电磁学

在CalculiX中，可以进行某些类型的电磁计算。这些包括：

静电计算：可以作为热计算的特例进行，参见第 6.9.13 节。
静磁计算。由于没有时间导数，电场和磁场之间的相互作用消失，磁场方程可以独立处理。
磁感应计算。这些是没有固定电荷且可以忽略位移电流的计算。这种计算的主要工业应用是感应加热。

本节只讨论最后两种应用。控制的麦克斯韦方程如下（在方程（735）中忽略了位移电流项）：

$\displaystyle \nabla \cdot \boldsymbol{D} = \rho$

(732)

$\displaystyle \nabla \times \boldsymbol{E} = - \frac {\partial \boldsymbol{B}}{\partial t}$

(733)

$\displaystyle \nabla \cdot \boldsymbol{B} = 0$

(734)

$\displaystyle \nabla \times \boldsymbol{H} = \boldsymbol{j}$

(735)

其中 $\boldsymbol{E}$ 是电场， $\boldsymbol{ D}$ 是电位移场， $\boldsymbol{B}$ 是磁场， $\boldsymbol{H}$ 是磁场强度， $\boldsymbol{ j}$ 是电流密度， $\rho$ 是电荷密度。这些场通过以下本构方程相互联系：

$\displaystyle \boldsymbol{D} = \epsilon \boldsymbol{E}$

(736)

$\displaystyle \boldsymbol{B} = \mu \boldsymbol{H}$

(737)

以及

$\displaystyle \boldsymbol{j} = \sigma \boldsymbol{E}.$

(738)

这里， $\epsilon$ 是介电常数， $\mu$ 是磁导率， $\sigma$ 是电导率。对于当前应用， $\epsilon$ 和 $\boldsymbol{ D}$ 不需要，方程（732）可以忽略。假设这些关系是线性和各向同性的，然而材料参数可以随温度变化。因此不考虑磁滞回线，这意味着只考虑顺磁材料和抗磁材料。目前不允许铁磁材料。

由于电磁学，需要一个额外的基本单位，即安培（A）。所有其他量可以用SI单位A、m、s、kg和K来表示，然而经常使用导出单位。这些单位的概述见表 17（V=伏特，C=库仑，T=特斯拉，F=法拉，S=西门子）。

**表 17:** 电磁应用常用单位
符号	含义	单位

I	电流	A

$\boldsymbol{E}$	电场	$\frac{\text{V}}{\text{m}} = \frac{\text{kg}.\text{m}}{\text{A}.\text{s}^3}$

$\boldsymbol{ D}$	电位移场	$\frac{\text{C}}{\text{m}^2} = \frac{\text{A}.\text{s}}{\text{m}^2}$

$\boldsymbol{B}$	磁场	${\text{T}} = \frac{\text{kg}}{\text{A}.\text{s}^2}$

$\boldsymbol{H}$	磁场强度	$\frac{\text{A}}{\text{m}}$

$\boldsymbol{ j}$	电流密度	$\frac{\text{A}}{\text{m}^2}$

$\epsilon$	介电常数	$\frac{\text{F}}{\text{m}} = \frac{\text{A}^2\text{s}^4}{\text{kg}\text{m}^3}$

$\mu$	磁导率	$\frac{\text{kg}.\text{m}}{\text{A}^2.\text{s}^2}$

$\sigma$	电导率	$\frac{\text{S}}{\text{m}}=\frac{\text{A}^2.\text{s}^3}{\text{kg}.\text{m}^3}$

P	磁标量势	A

V	电标量势	V $= \frac{\text{kg}.\text{m}^2}{\text{A}.\text{s}^3}$

$\boldsymbol{A}$	磁矢量势	$\frac{\text{kg}.\text{m}}{\text{A}.\text{s}^2}$

以下参考文献 [89] 和 [46] 被使用。在感应加热应用中，感兴趣的区域由待加热物体（=工件）、周围空气和提供电流的线圈组成，从而产生感应。可以假设线圈可以作为驱动力单独考虑，而不需要系统的反馈。这要求线圈配备调节系统，以抵消任何外部影响试图按用户意图修改电流的行为。

**图151：** 单连通体的电磁设置
$\begin{figure}\epsfig{file=em1.eps,width=10cm}\end{figure}$

让我们首先尝试理解物理上发生了什么。在最简单的情况下，待分析的体积由一个被空气包围的单连通体组成，如图 151 所示。如果体内任何虚构的闭合回路都可以在不离开体的情况下收缩到一个点，则该体是单连通的。例如，球体是单连通的，环不是。提供电流的线圈位于空气中。打开电流后，通过方程（735）产生磁场强度场，通过方程（737）产生磁场遍布各处，包括空气和体内。如果电流不随时间变化，这就构成了问题的解。

如果电流随时间变化，磁场也随之变化，通过方程（733738）在任何导电部分（即通常在体内，但不在空气中）产生电流（称为涡流）。这个电流通过方程（735）产生磁场强度场，方向与原始磁场强度场相反。因此，涡流阻碍体内磁场的建立。实际上，这意味着磁场不会立即建立，而是逐渐建立，就像由于热传递而导致的物体温度只能逐渐变化一样。事实上，这两种现象都用时间的一阶微分方程描述。涡流的欧姆损耗是工业感应加热应用中热生成的来源。

从这些考虑可以意识到，在体内（区域2，参见图 151；注意区域1和2与 [89] 中的顺序相反）需要计算电场和磁场，而在空气中只需考虑磁场（区域1）。因此，在空气中只需使用满足以下条件的标量磁势 P：

$\displaystyle \boldsymbol{H}=\boldsymbol{T_0} - \nabla P.$

(739)

这里， $\boldsymbol{T_0}$ 是线圈电流在无限自由空间中产生的磁场强度。 $\boldsymbol{T_0}$ 可以使用毕奥-萨伐尔关系 [29] 计算：

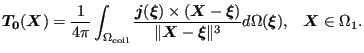$\displaystyle \boldsymbol{T_0}(\boldsymbol{X}) = \frac{1}{4 \pi } \int_{\Omega ... ...\xi } \Vert^3} d \Omega(\boldsymbol{\xi }), \;\;\; \boldsymbol{X} \in \Omega_1.$

(740)

这个积分计算量非常大，因此并行化非常重要。

体内场可以用矢量磁势 $\boldsymbol{A}$ 和标量电势 V 描述，满足：

$\displaystyle \boldsymbol{B}= \nabla \times \boldsymbol{A},$

(741)

$\displaystyle \boldsymbol{E}= -\frac{\partial \boldsymbol{A}}{\partial t} - \nabla V.$

(742)

实际上，方便地设 $V=\frac{\partial v}{\partial t}$ ，得到：

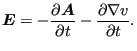$\displaystyle \boldsymbol{E}= -\frac{\partial \boldsymbol{A}}{\partial t} -\frac{\partial \nabla v}{\partial t}.$

(743)

这保证了生成的矩阵将是对称的。

**图152：** 多连通体的电磁设置
$\begin{figure}\epsfig{file=em2.eps,width=10cm}\end{figure}$

如果体是多连通的，计算域由三个区域组成。体（或多个体）仍然由区域2组成，未知量为 $\boldsymbol{A}$ 和。然而，空气必须分成两部分：一部分，如果与体相加，使它们成为单连通的。这是区域3，用矢量磁势 $\boldsymbol{A}$ 描述。假设区域3中没有导电线圈。剩余的空气是区域1，用标量磁势 P 描述。

在不同的区域中，需要求解不同的方程。在区域1中，电场不重要，因为没有电导。因此，只需计算磁场，只需满足方程（734）和（735）。使用方程（739）中的假设，方程（735）自动满足，因为它由 $\boldsymbol{T_0}$ 满足，梯度的旋度消失。剩下的方程是（734）。得到方程：

$\displaystyle \nabla \cdot \mu (\boldsymbol{T_0} - \nabla P) = 0.$

(744)

在区域2中，需要满足方程（733）、（734）和（735），使用方程（741）和（742）的方法。对方程（742）取旋度得到方程（733）。对方程（741）取散度得到方程（734）。将方程（741）和（742）代入方程（735）得到：

$\displaystyle \nabla \times \frac{1}{\mu } (\nabla \times \boldsymbol{A}) + \sigma \frac{\partial \boldsymbol{A} }{\partial t} + \sigma \nabla V = 0.$

(745)

矢量磁势 $\boldsymbol{A}$ 不能由方程（741)唯一定义。 $\boldsymbol{A}$ 的散度仍然可以自由定义。这里，我们采用库仑规范，即设：

$\displaystyle \nabla \cdot \boldsymbol{A}=0.$

(746)

注意，满足方程（735）自动满足电荷守恒，在区域2中表示为：

$\displaystyle \nabla \cdot \boldsymbol{j} =0,$

(747)

因为没有集中电荷。因此，对于单连通体，我们得到方程（744）（区域1）、（745）（区域2）和（746）（区域2）。实际上，方程（745）和（746）经常组合得到：

$\displaystyle \nabla \times \frac{1}{\mu } (\nabla \times \boldsymbol{A}) - \na... ...\boldsymbol{A} + \sigma \frac{\partial \boldsymbol{A} }{\partial t} + \sigma \nabla V = 0.$

(748)

然而，这不再等价于方程（735）的解，因此方程（747）的满足现在需要显式请求：

$\displaystyle \nabla \cdot \sigma ( \frac{\partial \boldsymbol{A} }{\partial t} + \nabla V) = 0.$

(749)

因此，现在要求解的方程是方程（748）（区域2）、（749）（区域2）和（744）（区域1）。

在区域3中，只需满足方程（734）和（735），其中 $\boldsymbol{j}=0$ （假设线圈在区域1中）。使用方程（741）中的假设，方程（734）自动满足，方程（735）现在简化为：

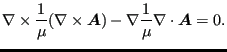$\displaystyle \nabla \times \frac{1}{\mu } (\nabla \times \boldsymbol{A}) - \nabla \frac{1}{\mu } \nabla \cdot \boldsymbol{A} = 0.$

(750)

界面上的边界条件为：

$\boldsymbol{B}$ 法向分量的连续性
$\boldsymbol{H}$ 切向分量的连续性，
没有电流垂直于边界流动，或者（ $\boldsymbol{n_i}$ 是区域i上的法向，指向离开该区域的方向）：

$\displaystyle \boldsymbol{B_1} \cdot \boldsymbol{n_1} + \boldsymbol{B_2} \cdot \boldsymbol{n_2} = 0,$

(751)

$\displaystyle \boldsymbol{H_1} \times \boldsymbol{n_1} + \boldsymbol{H_2} \times \boldsymbol{n_2} = 0$

(752)

和

$\displaystyle \boldsymbol{j_2} \cdot \boldsymbol{n_2}= 0$

(753)

所有这些都必须满足于 $\Gamma _{12}$ 。用磁矢量势 $\boldsymbol{A}$ 、电标量势 V 和磁标量势 P 表示，这相当于：

$\displaystyle \mu (\boldsymbol{T_0} - \nabla P) \cdot \boldsymbol{n_1} + (\nabla \times \boldsymbol{A}) \cdot \boldsymbol{n_2} =0,$

(754)

$\displaystyle (\boldsymbol{T_0} - \nabla P) \times \boldsymbol{n_1} + \frac{1}{\mu _1} ( \nabla \times \boldsymbol{A}) \times \boldsymbol{n_2} = 0$

(755)

和

$\displaystyle (\frac{\partial \boldsymbol{A} }{\partial t} + \nabla V)_2 \cdot \boldsymbol{n_2} = 0$

(756)

在 $\Gamma_{12}$ 上。为保证唯一性，电势必须在一个节点处固定， $\boldsymbol{A}$ 的法向分量必须沿 $\Gamma_{12}$ 消失 [89]：

$\displaystyle \boldsymbol{A} \cdot \boldsymbol{n_2}=0.$

(757)

为了获得上述方程的弱形式，将它们乘以试函数并积分。试函数用 $\delta \boldsymbol{A}, \delta V$ 和 $\delta P$ 表示。从方程（748) 开始，乘以 $\boldsymbol{\delta A}$ 并利用矢量恒等式：

$\displaystyle \nabla \cdot (\boldsymbol{a} \times \boldsymbol{b})=(\nabla \time... ...\boldsymbol{a}) \cdot \boldsymbol{b} - \boldsymbol{a} \cdot (\nabla \times \boldsymbol{b})$

(758)

$\displaystyle \nabla \cdot ( \alpha \boldsymbol{a} ) = \nabla \alpha \cdot \boldsymbol{a} + \alpha \nabla \cdot \boldsymbol{a}$

(759)

考虑在内（将 $\boldsymbol{b}= (\nabla \times \boldsymbol{A})/\mu$ 代入第一个矢量恒等式）：

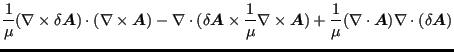	$\displaystyle \frac{1}{\mu } (\nabla \times \delta \boldsymbo... ...\frac{1}{\mu } (\nabla \cdot \boldsymbol{A}) \nabla \cdot (\delta \boldsymbol{A})$
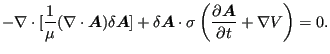	$\displaystyle - \nabla \cdot [ \frac{1}{\mu } (\nabla \cdot \boldsymbol{A} ) \d... ...\sigma \left( \frac{\partial \boldsymbol{A} }{\partial t} + \nabla V \right) = 0.$	(760)

积分得到（使用高斯定理，假设 $\Omega_2$ 没有自由边界，即没有不与 $\Omega_1$ 连接的边界）：

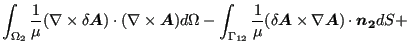	$\displaystyle \int _{\Omega _2} \frac{1}{\mu } (\nabla \times \delta \boldsymbo... ...\delta \boldsymbol{A} \times \nabla \boldsymbol{A}) \cdot \boldsymbol{n_2} dS +$
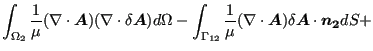	$\displaystyle \int _{\Omega _2} \frac{1}{\mu } ( \nabla \cdot \boldsymbol{A}) (... ...(\nabla \cdot \boldsymbol{A}) \delta \boldsymbol{A} \cdot \boldsymbol{n_2} dS +$
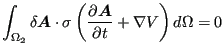	$\displaystyle \int _{\Omega _2} \delta \boldsymbol{A} \cdot \sigma \left( \frac{\partial \boldsymbol{A} }{\partial t } + \nabla V \right) d \Omega =0$	(761)

试函数也必须满足运动约束。因此， $\delta \boldsymbol{A} \cdot \boldsymbol{n_2}=0$ ，第二个面积分为零。

应用矢量恒等式

$\displaystyle (\boldsymbol{a} \times \boldsymbol{b}) \cdot \boldsymbol{n} = \boldsymbol{a} \cdot (\boldsymbol{b} \times \boldsymbol{n})$

(762)

以及方程（755）的边界条件，第一个面积分的被积函数可以写成：

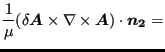	$\displaystyle \frac{1}{\mu } ( \delta \boldsymbol{A} \times \nabla \times \boldsymbol{A} ) \cdot \boldsymbol{n_2} =$
	$\displaystyle \frac{1}{\mu } \left ( \delta \boldsymbol{A} \cdot [ ( \nabla \times \boldsymbol{A}) \times \boldsymbol{n_2}] \right) =$
	$\displaystyle - \delta \boldsymbol{A} \cdot \left[ ( \boldsymbol{T_0} - \nabla \boldsymbol{P}) \times \boldsymbol{n_1} \right].$	(763)

因此，积分现在为：

$\displaystyle \int _{\Gamma _{12}} \left[ - \delta \boldsymbol{A} \cdot ( \bold... ...) + \delta \boldsymbol{A} \cdot ( \nabla P \times \boldsymbol{n_2}) \right] dS.$

(764)

应用同样的矢量恒等式进一步得到：

$\displaystyle \int _{\Gamma _{12}} \left[ - \delta \boldsymbol{A} \cdot ( \bold... ...) + \boldsymbol{n_2} \cdot ( \delta \boldsymbol{A} \times \nabla P) \right] dS.$

(765)

最后，使用矢量恒等式：

$\displaystyle \boldsymbol{n_2} \cdot (\delta \boldsymbol{A} \times \nabla P) = ... ...\boldsymbol{A})]-\boldsymbol{n_2} \cdot [ \nabla \times (P \delta \boldsymbol{A})]$

(766)

得到

$\displaystyle \int _{\Gamma _{12}} \left\{ - \delta \boldsymbol{A} \cdot ( \bold... ...\delta \boldsymbol{A})] - \boldsymbol{n_2} \cdot [ \nabla \times (P \delta \boldsymbol{A}) ] \right\} dS.$

(767)

假设区域3没有自由边界，最后一项消失。第一项可以解释为作用在界面上的体积力密度。第二项可以整合到弱形式中。

现在总结一下不同区域的最终弱形式。

表18： 单连通体的电磁问题

$\displaystyle \int_{\Omega_1} \nabla \delta P \cdot \mu \nabla P d\Omega - \int_{\Omega_1} \nabla \delta P \cdot \mu \boldsymbol{T_0} d\Omega = 0.$

(768)

$\displaystyle \int_{\Omega_2} (\nabla \times \delta \boldsymbol{A}) \cdot \frac{1}{\mu} (\nabla \times \boldsymbol{A}) d\Omega$

$\displaystyle \int_{\Omega_2} \nabla \cdot \delta \boldsymbol{A} \frac{1}{\mu} \nabla \cdot \boldsymbol{A} d\Omega$

$\displaystyle \int_{\Omega_2} \delta \boldsymbol{A} \cdot \sigma \frac{\partial \boldsymbol{A}}{\partial t} d\Omega$

$\displaystyle \int_{\Omega_2} \delta \boldsymbol{A} \cdot \sigma \nabla V d\Omega$

$\displaystyle \int_{\Gamma_{12}} \delta \boldsymbol{A} \cdot (\boldsymbol{T_0} \times \boldsymbol{n_2}) dS = 0.$

(769)

类似地，对于多连通体：

表19： 多连通体的电磁问题

区域1（标量磁势 P）：方程（768）

区域2（矢量磁势 A，标量电势 V）：方程（769）

区域3（矢量磁势 A）：

$\displaystyle \int_{\Omega_3} (\nabla \times \delta \boldsymbol{A}) \cdot \frac{1}{\mu} (\nabla \times \boldsymbol{A}) d\Omega$

$\displaystyle \int_{\Omega_3} \nabla \cdot \delta \boldsymbol{A} \frac{1}{\mu} \nabla \cdot \boldsymbol{A} d\Omega = 0.$

(770)

有关在CalculiX中实现这些方程的详细信息，请参见第节。