Ideal gas for large deformations

An ideal gas can also be modeled as a hyperelastic material. Indeed, the ideal gas law

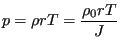$$p = \rho r T = \frac{\rho_0 r T}{J}$$ (379)

can also be written as

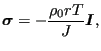$$\boldsymbol{\sigma } = - \frac{\rho_0 r T}{J} \boldsymbol{I},$$ (380)

where $\boldsymbol{\sigma }$ is the Cauchy stress and $\boldsymbol{I}$ is the identity tensor of second order. The Piola-Kirchhoff stress $\boldsymbol{S}$ amounts to:

$$\boldsymbol{S} = J \boldsymbol{F}^{-1} \cdot \boldsymbol{\sigma }... ...ldsymbol{F}^{-T} = - \rho_0 r T (\boldsymbol{F}^{T} \cdot \boldsymbol{F})^{-1},$$ (381)

or

$$\boldsymbol{S}= - \rho_0 r T \boldsymbol{C}^{-1}.$$ (382)

Using Equation (4.156) from [24] it is not difficult to prove that this stress can be derived from the free energy function

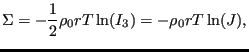$$\Sigma = - \frac{1}{2} \rho_0 r T \ln ( I_3)= -\rho_0 r T \ln(J),$$ (383)

where $I_3=J^2$ is the third invariant of the Cauchy-Green tensor $\boldsymbol{C}$. To obtain the material stiffness $\partial \boldsymbol{S}/\partial \boldsymbol{E}$ Equation (4.163) from [24] can be used.

In CalculiX this law can be used in any mechanical calculation provided the temperature is known. It is coded as a user material in routine umat_ideal_gas.f. In order to use this material, the constant $\rho _0 r$ should be given underneath a *USER MATERIAL,CONSTANTS=1 card. The name of the material has to start with IDEAL_GAS, the remaining 71 characters are at the free disposal of the user (a material name can be maximum 80 characters long). In addition, the parameter NLGEOM must be used on the *STEP card. Furthermore, the *PHYSICAL CONSTANTS card should be used to define the value of absolute zero temperature.