Deformation plasticity

Deformation plasticity is characterized by a one-to-one (bijective) relationship between the strain and the stress. This relationship is a three-dimensional generalization of the one-dimensional Ramberg-Osgood law frequently used for metallic materials (e.g. in the simple tension test) yielding a monotonic increasing function of the stress as a function of the strain. Because tensile and compressive test results coincide well when plotting the Cauchy (true) stress versus the logarithmic strain, these quantities are generally used in the deformation plasticity law. The implementation in CalculiX (keyword card *DEFORMATION PLASTICITY) implicitly uses the Abaqus interface in CalculiX for large deformations. The three-dimensional extension of the Ramberg-Osgood law reads [1]:

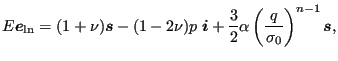$$E \boldsymbol{e}_{\text{ln}} = (1+\nu ) \boldsymbol{s } - (1-2 \n... ...+ \frac{3}{2} \alpha \left( \frac{q}{\sigma_0} \right) ^ {n-1} \boldsymbol{s },$$ (384)

where $\boldsymbol{e}_{\text{ln}}$ is the logarithmic strain (cf. beginning of Section 6), $\boldsymbol{\sigma }$ is the Cauchy stress, $\boldsymbol{i}$ is the identity tensor in spatial coordinates, $p:= -\boldsymbol{\sigma }: \boldsymbol{i}/3$ is the pressure, $\boldsymbol{s}=\boldsymbol{\sigma }+ p \boldsymbol{i}$ is the stress deviator and $q=\sqrt{3 \boldsymbol{s}: \boldsymbol{s}/2 }$ is the von Mises stress. $E$ and $\nu$ are Young's modulus and Poisson's coefficient, respectively (cf. *DEFORMATION PLASTICITY for the one-dimensional form).

The user should give the Ramberg-Osgood material constants $\sigma_0$, $n$ and $\alpha$ directly (by plotting a Cauchy stress versus logarithmic strain curve and performing a fit).