Theory

The finite element method is basically concerned with the determination of field variables. The most important ones are the stress and strain fields. As basic measure of strain in CalculiX the Lagrangian strain tensor E is used for elastic media, the deviatoric elastic left Cauchy-Green tensor for incremental plasticity, the logarithmic (or Hencky) strain [10] for some other plasticity models as deformation plasticity and Johnson-Cook hardening and linear strains where appropriate, i.e. for small deformations combined with small rotations. The Lagrangian strain satisfies ([27]):

$$E_{KL}=(U_{K,L}+U_{L,K}+U_{M,K} U_{M,L})/2,\;\;\;K,L,M=1,2,3$$ (2)

where $U_K$ are the displacement components in the material frame of reference and repeated indices imply summation over the appropriate range. In a linear analysis, this reduces to the familiar form:

$$\tilde{E}_{KL}=(U_{K,L}+U_{L,K})/2,\;\;\;K,L=1,2,3.$$ (3)

The deviatoric elastic left Cauchy-Green tensor is defined by ([90]):

$$\bar{b}^e_{kl}=J^{e-2/3}x^e_{k,K}x^e_{l,K}$$ (4)

where $J^e$ is the elastic Jacobian and $x^e_{k,K}$ is the elastic deformation gradient. Finally, the logarithmic strain satisfies:

$$e_{\text{ln}}:= \sum_{i} \ln \lambda_i \boldsymbol{n}_i \otimes \boldsymbol{n}_i,$$ (5)

where $\lambda_i^2$ are the eigenvalues of the Cauchy-Green tensor $\boldsymbol{C}:= \boldsymbol{F}^T \cdot \boldsymbol{F}$ and $\boldsymbol{n}_i$ are obtained from the eigenvectors $\boldsymbol{N}_i$ of $\boldsymbol{C}$ through

$$\boldsymbol{n}_i = \boldsymbol{R} \cdot \boldsymbol{N}_i,$$ (6)

where $\boldsymbol{R}$ is the rotation tensor obtained from the well known decomposition of the deformation gradient $\boldsymbol{F}$ into a product of an orthogonal matrix $\boldsymbol{R}$ and a symmetric matrix $\boldsymbol{U}$ in the form $\boldsymbol{F}= \boldsymbol{R} \cdot \boldsymbol{U}$. The above formulas apply to Cartesian coordinate systems.

The stress measure consistent with the Lagrangian strain is the second Piola-Kirchhoff stress $\boldsymbol{S}$. This stress, which is internally used in CalculiX for all applications (the so-called total Lagrangian approach, see [10]), can be transformed into the first Piola-Kirchhoff stress $\boldsymbol{P}$ (the so-called engineering stress, a non-symmetric tensor) and into the Cauchy stress $\boldsymbol{\sigma }$ (true stress). All CalculiX input (e.g. distributed loading) and output is in terms of true stress. The stress measures are related by:

$$\boldsymbol{P} = J \boldsymbol{F}^{-1} \cdot \boldsymbol{\sigma }$$ (7)

and

$$\boldsymbol{S} = J \boldsymbol{F}^{-1} \cdot \boldsymbol{\sigma } \cdot \boldsymbol{F}^{-T},$$ (8)

where $J=\det(\boldsymbol{F})$.

The treatment of the thermal strain depends on whether the analysis is geometrically linear or nonlinear. For isotropic material the thermal strain tensor amounts to $\overline{\alpha} \Delta T \boldsymbol{I}$, where $\overline{ \alpha}$ is the (secant) expansion coefficient, $\Delta T$ is the temperature change since the initial state and $\boldsymbol{I}$ is the second order identity tensor. For geometrically linear calculations the thermal strain is subtracted from the total strain to obtain the mechanical strain:

$$\tilde{E}_{KL}^{\text{mech}} = \tilde{E}_{KL} - \overline{\alpha} \Delta T \delta_{KL}.$$ (9)

In a nonlinear analysis the thermal strain is subtracted from the deformation gradient in order to obtain the mechanical deformation gradient. Indeed, assuming a multiplicative decomposition of the deformation gradient one can write:

$$d \boldsymbol{x} = \boldsymbol{F} \cdot d \boldsymbol{X} = \boldsymbol{F}_{\text{mech}} \cdot \boldsymbol{F}_{\text{th}} \cdot d \boldsymbol{X},$$ (10)

where the total deformation gradient $\boldsymbol{F}$ is written as the product of the mechanical deformation gradient and the thermal deformation gradient. For isotropic materials the thermal deformation gradient can be written as $\boldsymbol{F}_{\text{th}}=(1+\overline{\alpha} \Delta T) \boldsymbol{I}$ and consequently:

$$\boldsymbol{F}_{\text{th}}^{-1} \approx (1-\overline{\alpha} \Delta T) \boldsymbol{I}.$$ (11)

Therefore one obtains:

$$(F_{\text{mech}})_{kK} \approx F_{kK}(1-\overline{\alpha} \Delta T) = (1+u_{k,K})(1-\overline{\alpha} \Delta T)$$

$$\approx 1+u_{k,K}-\overline{\alpha} \Delta T.$$ (12)

Based on the mechanical deformation gradient the mechanical Lagrange strain is calculated and subsequently used in the material laws:

$$2 \boldsymbol{E}_{\text{mech}} = \boldsymbol{F}_{\text{mech}}^T \cdot \boldsymbol{F}_{\text{mech}} - \boldsymbol{I}.$$ (13)

Since the stretches $\lambda$ are the eigenvalues of the deformation gradient, subtracting $\overline{\alpha} \Delta T \boldsymbol{I}$ from $\boldsymbol{F}$ amounts to subtracting $\overline{\alpha} \Delta T$ from $\lambda = L/L_0 = 1 + \Delta L/L_0$. Therefore, the thermal strain get the meaning of a length change divided by an initial length. Infinitesimally one obtains:

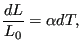$$\frac{dL}{L_0} = \alpha d T,$$ (14)

leading to

$$\frac{L-L_0}{L_0} = \int_{T_0}^{T} \alpha (\xi) d \xi$$

$$=: \overline{\alpha }(T) (T-T_0)$$

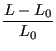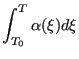$$= \overline{\alpha } (T) \Delta T,$$ (15)

from which

$$L = L_0 ( 1 + \overline{\alpha }(T) \Delta T.$$ (16)

Here, $T_0$ is the temperature for which the specimen length is $L_0$, $\alpha$ is the instantaneous or tangent expansion coefficient and $\overline{ \alpha}$ is the secant expansion coefficient. We observe that the extension is linear in the temperature. This is also the way in which the expansion coefficients are usually measured, i.e. with respect to the initial specimen length.

Notice that the same approach is taken in CalculiX for the calculation of the corotational logarithmic strain needed for an Abaqus User Material Routine. First, the thermal strain is subtracted from the total stretch to obtain the mechanical stretch and then the corational logarithmic mechanical strain is built:

$$\hat{E}_{\text{ln,mech}} = \sum_{i} \ln \lambda_{\text{mech},i} \boldsymbol{N}_i \otimes \boldsymbol{N}_i,$$ (17)

In Abaqus, however, it is obtained according to:

$$\hat{E}_{\text{ln,mech}} = \sum_{i} (\ln \lambda_i - \overline{\alpha} \Delta T) \boldsymbol{N}_i \otimes \boldsymbol{N}_i,$$ (18)

which implies

$$\frac{dL}{L} = \alpha d T,$$ (19)

leading to

$$\ln \frac{L}{L_0} = \int_{T_0}^{T} \alpha (\xi) d \xi$$

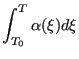$$= \overline{\alpha } (T) \Delta T,$$ (20)

or

$$L = L_0 \exp[\overline{\alpha }(T) \Delta T].$$ (21)

This establishes an exponential expansion relationship. This is fine, as long as the thermal strain was also measured according to Equation(19), i.e. with reference to the actual length. The latter approach, used by a lot of Finite Element codes requires linear expansion coefficients for linear calculations (using linear strain) and exponential ones for nonlinear geometric calculations (using logarithmic strain). The approach in CalculiX avoids this.