Next: Tension-only and compression-only materials. Up: Materials Previous: Plasticity with Johnson-Cook hardening. Contents
The theory and algorithms used to code the classical Mohr-Coulomb plasticity model are primarily taken from [100] and [21] and the references therein.
The Mohr-Coulomb plasticity is non-associative with a piecewise linear yield
surface ![]() an a piecewise linear plastic potential
an a piecewise linear plastic potential ![]() . The basic idea is
that the shear stress at which plastic flow occurs increases with increasing
pressure, similar to contact sliding. This is illustrated in Figure
140 showing the shear stress
. The basic idea is
that the shear stress at which plastic flow occurs increases with increasing
pressure, similar to contact sliding. This is illustrated in Figure
140 showing the shear stress ![]() versus normal stress
versus normal stress
![]() .
.
![]() are the principal
stresses.
are the principal
stresses.
The yield surface satisfies:
| (388) |
where ![]() is the cohesion. This is equivalent to (cf. Figure 140)
is the cohesion. This is equivalent to (cf. Figure 140)
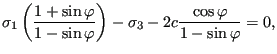 |
(389) |
or
where
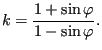 |
(391) |
![]() is called the friction angle. Similarly, the plastic potential is
defined by:
is called the friction angle. Similarly, the plastic potential is
defined by:
| (392) |
where
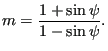 |
(393) |
![]() is called the dilation angle. It describes to what extent the volume of
the material changes due to shear motion. For a positive value of
is called the dilation angle. It describes to what extent the volume of
the material changes due to shear motion. For a positive value of ![]() the
volume increases, as for dense sand. For a negative value the volume
decreases, as for loose sand. In the latter case the grains fit better due to
the motion. You can easily illustrate this by pouring suger in a bowl. Shaking
the bowl the volume will decrease and more sugar will fit.
the
volume increases, as for dense sand. For a negative value the volume
decreases, as for loose sand. In the latter case the grains fit better due to
the motion. You can easily illustrate this by pouring suger in a bowl. Shaking
the bowl the volume will decrease and more sugar will fit.
As mentioned, the yield surface is piecewise linear, so the gradient of the surface is not continuous. This complicates matters. Now, looking at the yield surface and plastic potential it can be observed that it contains only principal stresses. Assuming the material to be elastically isotropic, this allows us to perform all operations in principal stress space, thereby reducing the tensors to vectors. This was first proposed in [20].
Replacing
![]() by
by ![]() for simplicity, the yield
surface as defined in Equation (390) defines in three-dimensional
space one of six faces of a irregular pyramid with central axis in
for simplicity, the yield
surface as defined in Equation (390) defines in three-dimensional
space one of six faces of a irregular pyramid with central axis in ![]() direction. The other faces correspond to sectors in which the order of
direction. The other faces correspond to sectors in which the order of
![]() is different.
is different.
Figure 141 shown a view
on a plane orthogonal to the ![]() axis and through the origin. The six
sectors are bordered by planes going through the x-, y- and z- axes and
containing the
axis and through the origin. The six
sectors are bordered by planes going through the x-, y- and z- axes and
containing the ![]() -axis. The cross section of this plane with the yield
surface is an irregular hexagon (dashed line). Since the principal stresses
can always be rearranged such that
-axis. The cross section of this plane with the yield
surface is an irregular hexagon (dashed line). Since the principal stresses
can always be rearranged such that
![]() it is sufficient to look at
that sector (labeled 1) and the neighboring ones (labeled 6 and 2).
it is sufficient to look at
that sector (labeled 1) and the neighboring ones (labeled 6 and 2).
Figure 142 shows the yield surface viewed from the apex and
looking in the direction of
![]() . In the sectors of interest the
normal to the surface
. In the sectors of interest the
normal to the surface
![]() is shown. For sector 1 this is
immediately clear from Equation (390) which can be written as
is shown. For sector 1 this is
immediately clear from Equation (390) which can be written as
![]() . A vector along
the interection lines of the pyramid faces is obtained by taking the cross
product of the normal of the neighboring faces,e.g.
. A vector along
the interection lines of the pyramid faces is obtained by taking the cross
product of the normal of the neighboring faces,e.g.
![]() . The apex of the pyramid is obtained
by substituting
. The apex of the pyramid is obtained
by substituting
![]() in Equation (390): it yields
in Equation (390): it yields
 |
(394) |
Therefore, the equation of the intersection line between section 6 and 1
satisfied
![]() . Its intersection with the plane
. Its intersection with the plane
![]() leads to
leads to
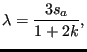 |
(395) |
yielding the location of point A in Figure 141. For point B one gets
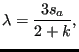 |
(396) |
which is farther away from the origin since ![]() . The normal to the
plastic potential surface is labeled
. The normal to the
plastic potential surface is labeled
![]() and amounts for sector 1
to
and amounts for sector 1
to ![]() . Similar expressions apply to the other sectors.
. Similar expressions apply to the other sectors.
The governing equations of an elastic material with Mohr-Coulomb plasticity read:
Elastic stress-strain relations
| (397) |
Internal variable relationship
| (398) |
Yield surface
| (399) |
Evolution equations
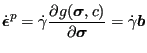 |
(400) |
Kuhn-Tucker equations
| (401) |
Consistency condition
| (402) |
Notice that in the above equatons
![]() and
and
![]() are vectors in principal space.
are vectors in principal space.
In order to explain the numerical procedure it is assumed that all variables
are known at the end of increment ![]() (corresponding to time
(corresponding to time ![]() ) and that
their values are sought at the end of increment
) and that
their values are sought at the end of increment ![]() (corresponding to time
(corresponding to time
![]() ). The input to the algorithm is a change on total strain
). The input to the algorithm is a change on total strain
![]() .
.
At first it is assumed that now plasticity occurs in the new increment, i.e.:
| (403) |
| (404) |
| (405) |
| (406) |
If
| (407) |
the solution is found. If not,
![]() and due to the Kuhn-Tucker equations
and due to the Kuhn-Tucker equations
![]() is
required. The stress at
is
required. The stress at ![]() can be written as:
can be written as:
| (408) | |||
| (409) | |||
| (410) | |||
| (411) | |||
| (412) |
In the last equation the evolution equation was used (flow rule). Defining
![]() , satisfying
the yield surface now requires:
, satisfying
the yield surface now requires:
| (413) |
Notice that
![]() points in the direction of the stress correction
w.r.t. the trial stress. In order to solve this equation a relationship between
points in the direction of the stress correction
w.r.t. the trial stress. In order to solve this equation a relationship between
![]() and
and
![]() is needed. Now,
is needed. Now,
![]() is defined as:
is defined as:
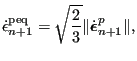 |
(414) |
from which:
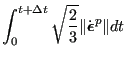 |
(415) | ||
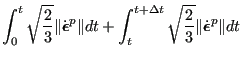 |
(416) | ||
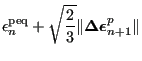 |
(417) | ||
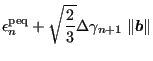 |
(418) | ||
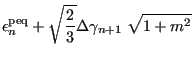 |
(419) |
Defining
![]() and
and
![]() the yield equation
now amounts to:
the yield equation
now amounts to:
| (420) |
This is a nonlinear equation in
![]() . Using the
Newton-Raphson procedure the first derivative is needed, which yields:
. Using the
Newton-Raphson procedure the first derivative is needed, which yields:
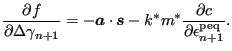 |
(421) |
Starting with an initial guess
![]() , one arrives at
, one arrives at
![]() by solving the equation:
by solving the equation:
| (422) |
or
![$\displaystyle \left [ - \boldsymbol{a} \cdot \boldsymbol{s} - k^*m^* \left . \f...
...a_{n+1}^{(k)} \boldsymbol{s} \right ] - k^* c(\epsilon_{n+1}^{\text{peq},(k)}),$](img1450.png) |
(423) |
where
| (424) |
This works as long a the return is to a face of the yield surface. Since the
return vector for sector 1 is
![]() one
can graphically plot the region in three-dimensional principal stress space
which is returned to the yield face in sector 1 (Figure 143). It
is the space for which
one
can graphically plot the region in three-dimensional principal stress space
which is returned to the yield face in sector 1 (Figure 143). It
is the space for which
| (425) |
This is called region I. The space within sector 1 in between region I and
sector 2 and underneath the apex is mapped onto the intersection line of face 1 and face 2 of the
yield surface (characterized by the equation
![]() ). It is characterized by the equations
). It is characterized by the equations
| (426) |
and is called region II of sector 1. Similary for the space in between region I and sector 6 and underneath the apex satisfying
| (427) |
This is region III. Finally, the region above the apex corresponding to
| (428) |
is returned to the apex and is called region IV.
Returning the trial stress to the intersection line of two yield faces implies that the final state has to satisfy both face equations. The equivalent plastic strain now satisfies:
| (429) |
and the yield surface equations amount to:
| 0 | (430) | ||
| (431) |
Applying Newton-Raphson now leads to:
![$\displaystyle [A] \cdot \begin{Bmatrix}\Delta \Delta \gamma_1 \\ \Delta \Delta \gamma_2 \end{Bmatrix} _{n+1}^{(k)} = \{B\},$](img1463.png) |
(432) |
where
![$\displaystyle [A]= \begin{bmatrix}- \boldsymbol{a_1} \cdot \boldsymbol{s_1} - k...
...on^{\text{peq}} } \right \vert _{\epsilon_{n+1}^{\text{peq},(k)}} \end{bmatrix}$](img1464.png) |
(433) |
and
![$\displaystyle \{B\}= \begin{Bmatrix}\boldsymbol{a_1} \cdot \left [ \boldsymbol{...
...oldsymbol{s_2} \right ] - k^* c(\epsilon_{n+1}^{\text{peq},(k)}) \end{Bmatrix}.$](img1465.png) |
(434) |
For a return to the apex the yield equations of sector 1, 2 and 6 have to be satisfied yielding 3 equations in 3 unknowns.
To calculate the consistent tangent the change of stress due to a change in total strain is needed. The change of stress in the present increment amounts to:
| (435) | |||
| (436) | |||
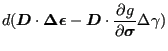 |
(437) | ||
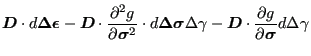 |
(438) | ||
| (439) |
Now, a relationship between
![]() and
and
![]() is needed. This is obtained from the yield equation:
is needed. This is obtained from the yield equation:
| (440) |
from which
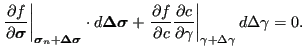 |
(441) |
Substituting the previously obtained expression for
![]() yields (dropping the bound of the derivatives to simplify the
notation; the derivatives are to be taken at the end of the present increment):
yields (dropping the bound of the derivatives to simplify the
notation; the derivatives are to be taken at the end of the present increment):
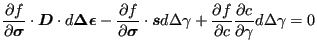 |
(442) |
from which
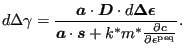 |
(443) |
Finally one obtains for the elastoplastic consistent tangent
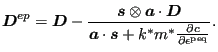 |
(444) |
The derivation of the elastoplastic consistent tangent for a return to the intersection between face 1 and face 2 is similar. Now, a change in stress increment amounts to:
| (445) |
A relationship between the change in
![]() and the change in
and the change in
![]() can again be obtained by considering the
adjacent yield
faces (i=1,2):
can again be obtained by considering the
adjacent yield
faces (i=1,2):
| (446) |
from which
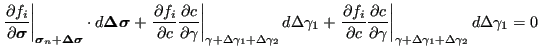 |
(447) |
or
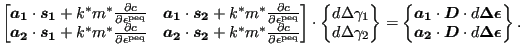 |
(448) |
Denoting the inverse of the left hand matrix by ![]() the solution of the
above system can be written as:
the solution of the
above system can be written as:
| (449) | |||
| (450) |
leading to:
| (451) |
The derivation for the return to the apex is similar (now three equations have to be satisfied).
The tangent derived here only applies to the normal directions. It has to be
complemented by a shear part ![]() in the form [20]:
in the form [20]:
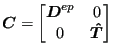 |
(452) |
where
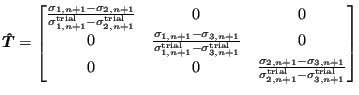 |
(453) |
Finally, the tangent matrix
![]() has to be transformed back into
the global system yielding
has to be transformed back into
the global system yielding
![]() :
:
| (454) |
where
![]() is the transformation matrix in equation (A5) in
[20]. Notice that equation (A6) in [20] is wrong and
has to be replaced by the equation above. Similarly the stress is to be
transformed into the global system by:
is the transformation matrix in equation (A5) in
[20]. Notice that equation (A6) in [20] is wrong and
has to be replaced by the equation above. Similarly the stress is to be
transformed into the global system by:
| (455) |