Next: Mohr-Coulomb plasticity. Up: Materials Previous: Incremental (visco)plasticity: additive decomposition Contents
In some sense this is a special case of the previous section, however, since it has been implemented as a Abaqus Material User Subroutine in CalculiX, establishing a relationship between the corotational Cauchy stress and the corotational logarithmic strain it can also be used for large deformations.
In principal, the Johnson-Cook model [43] proposes a yield curve for a conventional plasticity model with isotropic hardening in the form:
![$\displaystyle \sigma_{\text{vm}} = \left [A+B \epsilon_p^n \right ] \left [1+C ...
...dot{\epsilon}_p}{\dot{\epsilon}_0} \right ) \right ] \left [1-(T^*)^m \right ],$](img1360.png) |
(385) |
where
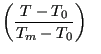 for for |
|||
| (386) |
Here,
![]() and
and ![]() are material constants. The
constant
are material constants. The
constant ![]() has the physical meaning of transition temperature, i.e. the
temperature above which the yield surface starts to shrink and
has the physical meaning of transition temperature, i.e. the
temperature above which the yield surface starts to shrink and ![]() has the
physical meaning of melt temperature, i.e. the temperature above which the
yield surface is reduced to zero. The model is meant to describe highly
dynamical phenomena such as explosions, bird strike in a jet engine etc.
has the
physical meaning of melt temperature, i.e. the temperature above which the
yield surface is reduced to zero. The model is meant to describe highly
dynamical phenomena such as explosions, bird strike in a jet engine etc.
For
![]() the logarithm becomes negative and
also for small
the logarithm becomes negative and
also for small
![]() convergence seems more difficult. Therefore,
Bernhardi and co-workers [57] have modified the above law for the
following special ranges of
convergence seems more difficult. Therefore,
Bernhardi and co-workers [57] have modified the above law for the
following special ranges of
![]() and
and
![]() to:
to:
![$\displaystyle \left [A+B \epsilon_p \delta ^{n-1} \right ] \left [1+C \ln \left...
...ght ]f(T^*) \;\;\; \dot{\epsilon}_p \ge \dot{\epsilon}_0,
\epsilon_p \le \delta$](img1374.png) |
|||
![$\displaystyle \left [A+B \epsilon_p^n \right ] \left [1+C \left(
\frac{\dot{\ep...
... \right ]f(T^*) \;\;\; \dot{\epsilon}_p < \dot{\epsilon}_0,
\epsilon_p > \delta$](img1375.png) |
|||
![$\displaystyle \left [A+B \epsilon_p \delta ^{n-1} \right ] \left [1+C \left(
\f...
...right ]f(T^*) \;\;\; \dot{\epsilon}_p < \dot{\epsilon}_0,
\epsilon_p \le \delta$](img1376.png) |
(387) |
where
![]() and
and ![]() is some small number. In CalculiX
is some small number. In CalculiX
![]() was taken.
was taken.
In the input deck the Johnson-Cook model is activated by the HARDENING=JOHNSON
COOK parameter on the *PLASTIC card. Underneath this card
the rate-independent terms are defined, i.e. the parameters
![]() and
and
![]() . If
. If ![]() no temperature dependence is taken into account. The rate
dependence has to be defined using a *RATE DEPENDENT
card with the parameter TYPE=JOHNSON COOK, listing underneath the parameters
no temperature dependence is taken into account. The rate
dependence has to be defined using a *RATE DEPENDENT
card with the parameter TYPE=JOHNSON COOK, listing underneath the parameters
![]() and
and
![]() .
.
The name of a material with Johnson-Cook hardening is not allowed to contain more than 69 characters.