下一个: 后处理灵敏度 上一级: 灵敏度分析 上一页: 预处理灵敏度 目录
灵敏度是在 results_se.c、mafillsmmain_se.c 和 objectivemain_se.c 程序中计算的。
在 results_se.c 程序中,确定了
![]() 。对于几何非线性计算(*STEP 卡上的参数 NLGEOM),导致内力的未扰动位移对应于前一静力步骤结束时的位移(如果有),并加上当前的指定位移。对于线性几何计算,未扰动的位移对应于零加上当前的指定位移。实际上,非零的指定位移在线性计算中会导致内力。因此,方程(809)中的项
。对于几何非线性计算(*STEP 卡上的参数 NLGEOM),导致内力的未扰动位移对应于前一静力步骤结束时的位移(如果有),并加上当前的指定位移。对于线性几何计算,未扰动的位移对应于零加上当前的指定位移。实际上,非零的指定位移在线性计算中会导致内力。因此,方程(809)中的项
![]() 可以在线性计算中替换为
可以在线性计算中替换为
![]() ,注意到只有非零的初始位移边界条件才会导致内力(而不是任何之前的位移)。results_se.c 必须在线性计算中调用的第二个原因是,每个积分点的材料切向
,注意到只有非零的初始位移边界条件才会导致内力(而不是任何之前的位移)。results_se.c 必须在线性计算中调用的第二个原因是,每个积分点的材料切向
![]() ,这是在 mafillsmmain_se.c 中建立刚度矩阵所需要的,也在 results_se.c 中确定。
,这是在 mafillsmmain_se.c 中建立刚度矩阵所需要的,也在 results_se.c 中确定。
mafillsmmain_se.c 程序计算外力的导数和刚度矩阵(以及类似矩阵)的导数:
| (934) |
被计算。
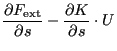 |
(935) |
被确定。
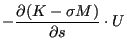 |
(936) |
被计算,其中 ![]() 是一个适当定义的标量。
是一个适当定义的标量。
出于计算效率的考虑,后面的项在单元级别计算,然后组装成全局矩阵。
最后一个主要程序 objectivemain_se.c 组装前面的信息以获得最终灵敏度。对于取向作为设计变量,这些灵敏度立即存储在 .dat 或 .frd 文件中。然而,对于几何(外部表面上节点的法向方向)作为设计变量的灵敏度,被保留用于在 sens_coor.c 中进行进一步后处理。
对于目标函数 ![]() ,总灵敏度
,总灵敏度
![]() 被写为
被写为
![]() 。因此,目标函数被用于项
。因此,目标函数被用于项
![]() 和
和
![]() 。objectivemain_se.c 程序根据目标函数分为几部分:
。objectivemain_se.c 程序根据目标函数分为几部分:
通常,目标函数不一定适用于整个结构,例如可以将结构的一部分的质量定义为设计变量。在这种情况下,所有其他元素被停用。这在 actidef.f 程序中完成。这适用于所有只包含部分结构的目标函数。
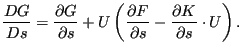 |
(937) |
右侧第一项的计算方式与质量在 objective_shapeener_dx.f 程序中的计算方式类似。右侧括号中的项已经在 results_se.f 和 mafillsmmain_se.f 中确定。将其与前一静力步骤的位移相乘并加上第一项得到灵敏度(objective_shapeener_tot.f)。
对于非线性几何计算,方程(810)简化为:
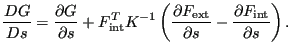 |
(938) |
现在,
![]() 通过求解方程组
通过求解方程组
![]() 来计算。其余操作与线性情况类似。
来计算。其余操作与线性情况类似。
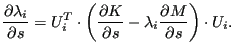 |
(939) |
从 mafillsmmain_se.f 中已经确定了右侧括号中的部分。因此,固有频率的灵敏度只需要与振型相乘。这在 objective_freq.f 和 objective_freq_cs.f(循环对称)中完成。
对于振型的灵敏度(仅针对取向作为设计变量计算),相关方程是方程(814),也可以写成:
假设灵敏度是振型的线性组合:
导致 ![]() 的以下表达式:
的以下表达式:
和 ![]() 。后者方程来自质量归一化条件
。后者方程来自质量归一化条件
![]() 的求导。实际上,得到:
的求导。实际上,得到:
因为 ![]() 是对称的且不依赖于材料的取向。这意味着
是对称的且不依赖于材料的取向。这意味着
![]() 与
与 ![]() 正交。从数学上也可以这样解释:方程(940)的解可以看作是一个特解加上齐次解的任意倍数。齐次解是
正交。从数学上也可以这样解释:方程(940)的解可以看作是一个特解加上齐次解的任意倍数。齐次解是 ![]() ,特解是通过其他振型的线性组合获得的,这些振型与
,特解是通过其他振型的线性组合获得的,这些振型与 ![]() 正交(因为 K 和 M 是对称的)。现在,方程(943)表示解与
正交(因为 K 和 M 是对称的)。现在,方程(943)表示解与 ![]() 正交,因此只剩下具有方程(942)中系数的特解。
正交,因此只剩下具有方程(942)中系数的特解。
的确定是直接的,基于在 mafillsmmain_se.f 中计算的表达式和固有频率的灵敏度。
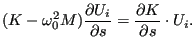 |
(945) |
并且需要对每个设计变量求解一个方程组。然而,系统矩阵不变,所以矩阵的 LU 分解只需要做一次。
对于取向作为设计变量,频率灵敏度存储在 .dat 文件中,而振型和/或格林函数的灵敏度存储在 .frd 文件中(frd_sen.c,从 objectivemain_se.c 调用)。对于几何作为设计变量,只确定频率灵敏度。它们没有存储在 objectivemain_se.c 中,因为它们可能需要在 sensi_coor.c 中进行进一步后处理。
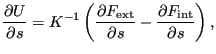 |
(946) |
对于几何非线性计算和
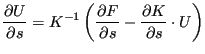 |
(947) |
对于几何线性计算。在这两种情况下,右侧括号中的项(我们称之为 ![]() )已经在之前计算过了。因此,完整的右侧通过求解
)已经在之前计算过了。因此,完整的右侧通过求解 ![]() 对每个设计变量来确定。由于系统的矩阵不依赖于设计变量,它只需要 LU 分解一次。
对每个设计变量来确定。由于系统的矩阵不依赖于设计变量,它只需要 LU 分解一次。
对于取向设计变量,结果从自由度转换到(节点,方向)表示在 resultsnoddir.f 中,并存储在 .frd 文件中的 frd_sen.c。对于几何设计变量,结果在 objective_disp_dx.f 中处理。这是因为几何设计变量的位移几何函数定义为所有设计节点位移平方和的平方根。离开 objective_disp_dx 后,结果被保留用于进一步后处理。
| (948) |
即,应力 S 通常是设计变量的直接函数,并通过位移间接成为函数。实际上,应力是材料常数与位移对几何的导数的"乘法"结果。
对于几何设计变量,需要评估两项
![]() 和
和
![]() ,即保持节点位移不变而改变几何会导致应力变化,以及保持几何不变而改变位移。
,即保持节点位移不变而改变几何会导致应力变化,以及保持几何不变而改变位移。
对于取向设计变量
![]() ,因为应力变化仅来自材料定律。
,因为应力变化仅来自材料定律。
对于几何设计变量,未扰动状态的应力在 resultsstr.c 中计算,而对 s 的导数在 stress_sen_dx.f 中计算,对 U 的导数在 stress_sen_dv.f 中计算。方程(810)的计算与第 6.9.23 节中从左到右的解释完全相同,即首先计算
![]() ,然后继续括号中的表达式。
,然后继续括号中的表达式。
对于取向设计变量,灵敏度可以写成
 |
(949) |
其中
![]() 被近似为
被近似为
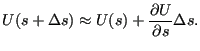 |
(950) |
因此,应力灵敏度需要位移灵敏度的知识。这在前一项中已经处理过。对于取向设计变量,上述操作需要 resultsnoddir.f 和 resultsstr.c 程序(及其子程序)。结果(即所有节点关于各向异性取向变化的 von Mises 应力灵敏度)存储在 frd 文件中。
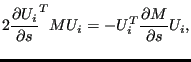 |
(951) |
和 ![]() 现在满足:
现在满足:
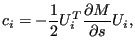 |
(952) |
而不是为零。定义
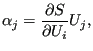 |
(953) |
得到模态 ![]() 的应力灵敏度:
的应力灵敏度:
![$\displaystyle \frac{d S}{d s} = \frac{\partial S}{\partial s} + c_i \alpha_i + ...
MN|...bda_i -\lambda_j} \right) \left[ U_j^T \frac{\partial F_i}{\partial s} \right].$](img3086.png) |
(954) |