Postprocessing the sensitivity

Postprocessing is only done for geometrical design variables. The postprocessing procedure is coded in sensi_coor.c and feasibledirection.c and consists of the following steps:

• Changing from a discrete gradient field to a continuous gradient field (sensi_coor.c).
• Backward filtering the sensitivities (sensi_coor.c).
• Calculating the geometrical constraints defined for the design variables (feasibledirection.c).
• Modifying the sensitivities due to constraint conditions (feasibledirection.c).
• Forward filtering of the sensitivities (feasibledirection.c).
• Creating a transition region from the design node region to its complement (feasibledirection.c).

Now the steps are treated in more detail:

• The sensitivity for geometric design variables is calculated by moving each design variable an infinitesimal distance in a direction normal to the external surface. Through the shape functions this motion extends across an area consisting of all external faces to which the design node belongs. Now, the resulting discrete or continuous gradient field $d G/d \boldsymbol{s}$ is transformed into a continuous gradient field $d g/d \boldsymbol{s}$ by

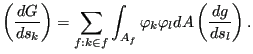  $$\left( \frac{d G}{d s_k } \right)= \sum_{f:k \in f} \int_{A_f} \varphi_k \varphi_l d A \left ( \frac{d g}{d s_l } \right) .$$ (955)

  
  

  The continuous gradient field is the sensitivity with respect to a Dirac delta function perturbation of the design surface at the node at stake. Both fields are coupled by the surface mesh mass matrix $M_A$. Therefore, to get the continuous gradient field the calculated sensitivities are multiplied with the inverse of the surface mesh mass matrix:

  $$\frac{dg}{d \boldsymbol{s} } = M_A^{-1} \frac{dG}{ds}.$$ (956)

  
  

• The filtering which is done after the sensitivity analysis and after the calculation of the feasible direction follows the idea of vertex morphing. This means that conceptually an additional control field $z$, apart from the design variables $s$, is introduced with the size of the number of design variables on which the mathematical optimization problem is solved. This control field is connected with the design variables by the following formula

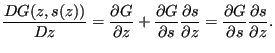  $$\frac{DG(z,s(z))}{Dz} = \frac{\partial G}{\partial z} + \frac{\pa... ...al s}{\partial z} =\frac{\partial G}{\partial s} \frac{\partial s}{\partial z}.$$ (957)

  
  

  Since a change in control field does not alter the geometry and hence the design response G, the partial derivative $\partial G/\partial z =0$. The expression $\partial s/\partial z$ can be regarded as a smoothing operator (filter) between the design variables and the control field. In vertex morphing this filtering operation has to be done twice. First, after the sensitivity analysis (sensi_coor.c), called backward filtering, in order to transform the sensitivities calculated at the design variables to the control field. The output in the frd file is the unfiltered sensitivity at the design variables as well as the filtered one, which can be interpreted as the sensitivity on the control field. And a second time to map the final feasible direction back to the nodal design variables, called forward filtering, which is done in feasibledirection.c. Again, two output fields are written in the frd file: the feasible direction calculated on the control field and the forward filtered feasible direction on the nodal design variables.

  For the filtering itself two different filters are available, an explicit and an implicit one. Ragarding the explicit filter, independent if backward or forward filtering is done, the sensitivity values at a given node are thereby replaced by a weighted sum of the sensitivities of the nodes within a sphere with a user-defined radius. The weighting function is 1 at the node at stake and decreases radially in a user-defined way to zero at the edge of the sphere:

  $$\frac{dG}{dz} = \frac{dG}{ds} \frac{ds}{dz} = \frac{dG}{ds} A = A^T \frac{dG}{ds},$$ (958)

  
  

  where $A$ is the resulting smoothing matrix mapping field $z$ into a smoother field $s$. The filtering can also be performed implicitly by elliptic partial differential equations whose inverse operator is a local smoother:

  $$(\boldsymbol{I} - \epsilon \nabla^2) s = z,$$ (959)

  
  

  leading to (through the chain rule):

  $$(\boldsymbol{I} - \epsilon \nabla^2) \frac{dG}{dz} = \frac{dG}{ds}.$$ (960)

  
  

  Notice that field $s$ is smoother than field $z$ and, consequently, field $\frac{dG}{dz}$ is smoother than field $\frac{dG}{ds}$. $\epsilon$ is a scalar penalizing high spatial variations and is also called the filter radius. Applying a standard finite element discretization scheme leads to:

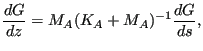  $$\frac{dG}{dz} = M_A ( K_A+M_A)^{-1} \frac{dG}{ds},$$ (961)

  
  

  where

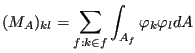  $$(M_A)_{kl} = \sum_{f:k \in f} \int_{A_f} \varphi_k \varphi_l d A$$ (962)

  
  

  and

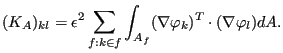  $$(K_A)_{kl} = \epsilon^2 \sum_{f:k \in f} \int_{A_f} (\nabla \varphi_k)^T \cdot (\nabla \varphi_l) d A.$$ (963)

  
  

  The gradient is to be projected into the design faces. As in the explicit filter method, the filter radius is a user-defined parameter controlling the smoothness of the filtered sensitivities. A complete filtering cycle than consists of:

  1. applying an explicit or implicit filter, respectively Equation (958) and Equation (960), to obtain $dG/dz$ from $dG/ds$. This is called backward filtering.
  2. convert the discrete field $dG/dz$ into a continuous field $dg/dz$ by equation (956).
  3. apply a scalar multiple of $dg/dz$ as mesh modification and revert to the $s$-field using $s=A z$ in the explicit case or Equation (959) for the implicit case. This is called forward filtering.

  For the complete derivation of the explicit and implicit filtering methods the interested user is referred to [7]. If the parameter DIRECTION WEIGHTING is active on the *FILTER card the sensitivity values at a node i are replaced by a weighted sum of the sensitivities at the nodes j within the sphere multiplied by the scalar product of the normal vector at j and the normal vector at i.

• If the parameter BOUNDARY WEIGHTING=YES is selected on the *FILTER card the sensitities are linearly decreased to zero at the edge of the design domain. This edge is defined by all nodes which are not design variables but belong to external faces which contain at least one design variable. If a design node lies within a user-defined boundary weighting distance from this edge a linear reduction proportional to the actual distance is applied. This assures a smooth transition of the sensitivities to zero at the edge of the design domain.